Planimetria - romb w kole Gosia: W romb o kącie ostrym 60⁰ wpisano okrąg. Punkty styczności okręgu z bokami rombu tworzą czworokąt ABCD o polu 3√3 a) uzasadnij, że czworokąt ABCD jest prostokątem; b) oblicz pole rombu.

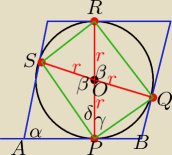
Basia: PS² = r²+r²−2r*r*cosβ = 2r²−2r²*cos120 = 2r²−2r²*(−¹₂) = 3r² PS = r√3 analogicznie liczysz QR i stwierdzasz, że QR = PS SR² = r²+r²−2r*r*cos(180−β) = 2r²−2r²*cos60 = 2r²−2r²*¹₂ = r² SR = r analogicznie liczysz PQ i stwierdzasz, że PQ = SR mamy więc na pewno równoległobok a kąty QPS; PSR; SRQ i RQP to kąty wpisane oparte na średnicach ⇒ te kąty są proste czyli mamy prostokąt r*r√3 = 3√3 r² = 3 r = √3

	2r
sinα =
	a

	2√3
sin60 =
	a

√3		2√3
	=
2		a

a = 4 P_rombu = a²*sin60 podstaw i policz

Gosia: Dziękuję

Krzysztof : Styczne poprowadzone z jednego punktu maja ta sama długość więc APS jest trojkatem RÓWNOBOCZNYM. Co za tym idzie kat SPQ jest prosty co kończy dowód że jest to prostokąt.

Krzysztof : AP = SP i PO = SO więc czworokat APOS jest deltoidem co za tym idzie alpha = beta a to rozwiązanie jest do dupy.

Grzesiek: Krzysztof pisze bzdury. APOS faktycznie jest deltoidem ale wynika stąd że alpha + beta = 180 czyli beta = 120. Wynik jest poprawny ale rozwiązanie jakby dookoła.