6 maj 21:59
gosc: W zad 11 doszedłem do teog co dalej? (x−1)2 (x+1)2(x2+1)? czy może wcześniej coś zauwazyc?
6 maj 22:02
Basia:
x jest całkowita i nieparzysta ⇒ x = 2k+1
x6 − x4 − x2 + 1 =
x4(x2−1)−(x2−1) =
(x2−1)(x4−1) = (x2−1)(x2−1)(x2+1) = (x2+1)(x−1)2(x+1)2 =
(4k2+4k+1+1)(2k)2(2k+2)2 =
2(2k2+2k+1)*4k2*4(k+1)2 = 32(2k2+2k+1)*k2*(k+1)2
6 maj 22:14
Saizou :
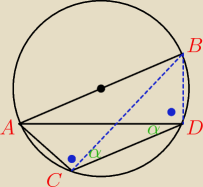
co do 9
zauważ że lACl=lBDl− jest to trapez równoramienny
6 maj 22:21
gosc: Dzięki!
6 maj 22:27
Saizou : ale to tylko wskazówka
i prawi koniec zadania
6 maj 22:28
gosc: Tak własnie zauważyłem ten trapez, ale nie zczaiło się o tym trojkącie prostokątnym...
6 maj 22:47
gosc: co tzn że zbiór wartości funkcji jest dwuelementowy? do zad 24
7 maj 00:50
gosc: Prosiłbym także kogoś o zad 14, 17 i 20
7 maj 00:54
gosc: zobaczy ktoś?
7 maj 11:24
gosc: może ktoś jeszcze da rade? zależy mi na tym...
7 maj 20:48