Wartość bezwzględna robertn5012: Rozwiąż nierówność |x²+6x−7|>6+|x+7|

robertn5012: no okej a w jakich przedziałach rozpatrywałeś te nierówności? bo ja (−∞;−7), (−7;1) i (1;+∞)

robertn5012: i rozpatruję trzy przypadki i tak sobie narysowałem tą parabole i jest mniejsza od zera w przedziale (−7;1)

robertn5012:

piotrek: −4 −5 −3 + 6

Mila: Jutro rozwiążę.

Basia: x²+6x−7 = 0 Δ = 36+28 = 64

	−6−8
x1 =		= −7
	2

	−6+8
x2 =		= 1
	2

czyli trzeba rozważyć przedziały: (−∞;−7> (−7;1) <1:∞) 1. x∊(−∞;−7> ⇒ |x²+6x−7| = x²+6x−7 ∧ |x+7| = −(x+7) = −x−7 i mamy nierówność x²+6x−7 > 6−x−7 x²+7x−6 > 0 Δ = 49 + 24 = 73

	−7−√73
x1 =
	2

	−7+√73
x2 =
	2

	−7−√73		−7+√73
x∊[ (−∞;		)∪(		;+∞) ]∩(−∞;−7>
	2		2

−7+√73		−7+√73
	> −7 czyli jest oczywiste, że (		;+∞)∩(−∞;−7>∅
2		2

natomiast

−7−√73
	< −7 (łatwo sprawdzić)
2

czyli mamy

	−7−√73
x∊(−∞;		)
	2

2. x∊(−7;1) ⇒ |x²+6x−7| = −(x²+6x−7) = −x²−6x+7 ∧ |x+7| = x+7 mamy nierówność −x²−6x+7 > 6+x+7 −x² − 7x −6 > 0 /*(−1) x² + 7x + 6 < 0 Δ = 49 − 24 = 25

	−7−5
x1 =		= −6
	2

	−7+5
x2 =		= −1
	2

x∊(−6; −1)∩(−7;1) czyli mamy x∊(−6;−1) 3. x∊<1;+∞) ⇒ |x²+6x−7| = x²+6x−7 ∧ |x+7| = x+7 mamy nierówność x²+6x−7 > 6+x+7 x² + 5x − 20 > 0 Δ = 25+80 = 105

	−5−√105
x1 =
	2

	−5+√105
x2 =
	2

	−5−√105		−5+√105
x∊ [(−∞;		)∪(		;+∞)]∩<1;+∞)
	2		2

−5−√105
	< 0 < 1
2

czyli

	−5−√105
(−∞;		)∩<1;+∞) = ∅
	2

−5+√105
	> 1 (znów łatwo sprawdzić)
2

czyli mamy

	−5+√105
x∊(		; +∞)
	2

ostatecznie:

	−7−√73		−5+√105
x∊x∊(−∞;		)∪(−6;−1)∪(		; +∞)
	2		2

liczby dość paskudne; sprawdź czy się nie pomyliłam w rachunkach i czy Ty się nie pomyliłeś przepisując treść zadania

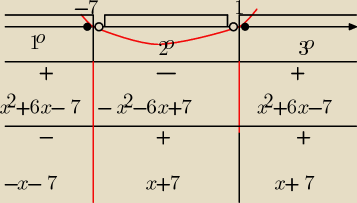
Gustlik: |x²+6x−7|>6+|x+7| ↓ ↓ x=−7 v x=1 x=−7 ← m. zerowe wyrażeń w modułach Metoda "osi i tabelki" − skorzystam z obliczeń Basi − tą metodą o wiele łatwiej układa się założenia, bo widać w tabelce, co sie robi. 1^o) x²+6x−7>6+(−x−7) ⋀ zał. x∊(−∞, −7> 2^o) −x²−6x+7>6+(x+7) ⋀ zał. x∊(−7, 1) 3^o) x²+6x−7>6+(x+7) ⋀ zał. x∊<1, +∞) Dalsze obliczenia jak u Basi. Odp. 1^o) U 2^o) U 3^o)

Mila: Basia, Gustlik .Pozdrawiam i podziwiam. Właśnie chciałam to teraz dopiero rozwiązać.