 zadanie maturalne za 6 pkt, matematyka rozszerzona
Miara największego kąta w trójkącie jest dwa razy większe od miary jego najmniejszego kąta.
Oblicz długości boków tego trójkąta, jeżeli są one kolejnymi liczbami naturalnymi.
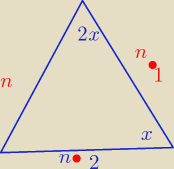
żeby było śmiesznie, nie potrafiłem dodać znaku "dodać" więc czerwona kropka oznacza "plus"
czyli boki trójkąta mają miary : n, n+1, n+2
1o
za pomocą twierdzenia sinusów mogę zapisać równość:
zadanie maturalne za 6 pkt, matematyka rozszerzona
Miara największego kąta w trójkącie jest dwa razy większe od miary jego najmniejszego kąta.
Oblicz długości boków tego trójkąta, jeżeli są one kolejnymi liczbami naturalnymi.
żeby było śmiesznie, nie potrafiłem dodać znaku "dodać" więc czerwona kropka oznacza "plus"
czyli boki trójkąta mają miary : n, n+1, n+2
1o
za pomocą twierdzenia sinusów mogę zapisać równość:
| n | n+2 | n+2 | |||
= | ⇔ cosx = | ||||
| sinx | sin2x | 2n |
| n+2 | ||
n2 = (n+1)2 + (n+2)2 − 2(n+1)(n+2) | ||
| 2n |

| n+2 | ||
n2=(n+1)2+(n+2)2−2(n+1)(n+2)* | ||
| 2n |
| (n+2)2(n+1) | ||
n2+6n+5= | ||
| n |
 takiego prostego równania nie potrafić rozwiązać, to znak że za dużo dzisiaj maty... hehe
@asdf, tak, zapomniałem o dziedzinie na samym początku, nie stworzy się trójkąta, który
będzie miał zerowy bok, zatem n>0
takiego prostego równania nie potrafić rozwiązać, to znak że za dużo dzisiaj maty... hehe
@asdf, tak, zapomniałem o dziedzinie na samym początku, nie stworzy się trójkąta, który
będzie miał zerowy bok, zatem n>0