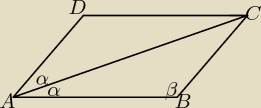
e blogther: Prosze o sprawdzenia poprawnosci wyniku koncowego Podstawa˛ graniastosłupa prostego jest romb, którego krótsza przekatna ma długosc c, a kat ostry miare 2α. Pole przekroju wyznaczonego przez krawedz boczna graniastosłupa i dłuzsza przekatna podstawy wynosi P. Oblicz długosc dłuzszej przekatnej graniastosłupa. jest troche liczenia wiec napisze najistotniejsze rzeczy β = 180^o − 2α BD = c AD = a

	c
a =
	2(1 − cos2α)

	√1 + cos2α
AC = c
	√1 − cos2α

pole przekroju to P = AC * CC' CC' − wsokosc graniastsłupa i jednoczescie krawedz boczna

	P
CC' =
	AC

AC' dłuzsza przekatna graniastosłupa

	√c4(1 + cos22α) + P2(1 − cos2α)
AC' =
	c√1 − cos22α

blogther: up

blogther: mam juz

blogther: to nie ja napisałem o 21:04

blogther: podszywanie sie pod ine osoby jest smieszne ale pod moj nick juz nie

blogther: no ja mam na kompie ale CI nie dam cFelu

blogther: jeszcze przez przypadke napisałem ci duzej litery jełopie jeden

blogther: ktos sie bawi moim nickiem

blogther: sory, to ja.

pigor: hmm ... ja widzę to np. tak : niech x, H − długość dłuższej przekątnej rombu i wysokości graniastosłupa odpowiednio , to d=√x²+H²=? − szukana długość dłuższej przekątnej graniastosłupa, wtedy z warunków zadania : ^x₂=^c₂ctgα ⇒ x=c ctgα ⇒ x²=c²ctg²α , zaś Hx=P ⇒ H c ctgα=P ⇒ H=¹_c P tgα ⇒ H²=¹_c² P²tg²α , zatem d²=c²ctg²α+¹_c² P²tg²α ⇒ ⇒ d=√c²ctg²α+c⁻² P²tg²α i dalej nie wiem czy warto coś z tym robić . ...

blogther: no wiem ze to ty cfeloksie

blogther: w opowiedzi jest to zapisane ze

	√c4 + P2tg2α
AC =
	c*tgα

blogther: wyniki sa troche podobne ale nie chce mi sie udowadniac dodatkowo takiej tozsamosci

pigor: ... masz rację , bo mnie też , ale na pierwszy rzut oka to samo . ...