Zadanie dla Shiro psik: Zadanie dla mojego kolegi ( nie musicie zaglądać , ty Shiro musisz) uzasadnij , ze 10(11⁹ + 11⁸ + 11⁷ +...11² + 12) + 1 jest równe 11¹⁰. Zapisuję to jako : 10(11⁹ + 11⁸ + 11⁷ +...11² + 11¹ + 1) + 1 Zauważam ciąg geometryczny q (iloraz ciągu) = 11 pierwszy wyraz ciągu: a₁ = 1 1 + 11 + 11² + ... + 11⁸ + 11⁹ Korzystam ze wzoru na sumę ciągu geometrycznego:

	1−qn		1−q10		1−1110
Sn = S10 = a1 *		= 1 *		= 1 *		=
	1−q		1−q		1−11

	1−1110
=
	−10

Na razie zostawię to w takiej postaci, bo z licznikiem nic konkretnego nie zrobię. Podstawiam teraz tę wartość zamiast nawiasu.

	1−1110
10(		) + 1 = − (1−1110) + 1 = − 1 + 1110 + 1 = 1110 c.n.u
	−10

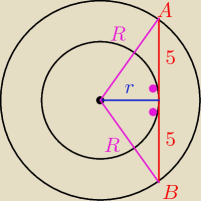
psik: Kolejne : Dane sa dwa okręgi o wspólnym środku. cięciwa wiekszego okregu styczna do mniejszego ma 10cm dlugosci. Oblicz pole pierscienia kolowego wyznaczonego przez te okręgi.

1
	|AB| = 5 cm
2

Pole dużego okręgu oznaczę jako P₁ Pole małego okręgu jako P₂ Pole pierścienia to P₁ − P₂ (pole dużego odjąć małego) P₁ = πR² P₂ = πr² z tw. Pitagorasa r² + 5² = R² r² = R² − 25 zatem podstawiając to do P₂ otrzymujemy P₂ = π( R² − 25 ) P₁ − P₂ = πR² − πR² + 25π = 25π [cm²].

Shiro: Rozwiąż równanie: (−2¹¹ * 8 + 4⁷ * 9x − 8¹⁰x/4⁸) : 4⁷ = − 3² plox :3

psik: mm

810x   (−211 * 8 + 47 * 9x − )   48
	= −32 | * 47
47

	23*10x
(−211 * 23 + 22*7 * 9x −		) = −9 * 47
	22*8

	230x
(−211+3 + 214 * 9x −		) = −9 * 47
	216

−2¹⁴ + 2¹⁴ * 9x − 2¹⁴x = −9 * 2¹⁴ wyciągam 2¹⁴ przed nawias 2¹⁴(−1+9x − x) = −9*2¹⁴ | : 2¹⁴ 8x − 1 = −9 8x = −8 x = −1 Plox <3

psik: Kolega ma zadania na 6 a ja się dowartościowuję że umiem takie zadania zamiast uczyć do matury

Shiro: W układzie równań : 2x−y=12−2a ax+y=8a tak dobierz wartości liczby a, aby rozwiązaniem układu była para liczb przeciwnych

psik: yeah muszę więc otrzymać x= −y podstawiam za x −2y−y=12−2a −ya + y = 8a −3y=12−2a y(−a + 1) = 8a

	8a
z drugiego równania mam y =
	1−a

podstawiam do I równania

	8a
−3(		) = 12 − 2a
	1−a

−24a
	= 12 − 2a | * (1−a)
1−a

−24a = 12 − 12a −2a + 2a² 2a² − 14a + 24a + 12 = 0 2a² + 10a +12 = 0 | :2 a² + 5a + 6 = 0 F.kwadratowa, liczę deltę (Δ) Δ = 5² − 4*1*6 = 25 − 24 = 1 √Δ = √1 = 1 Liczę pierwiastki :

	−5 +1
a1 =		= −2
	2

	−5 − 1
a2 =		= −3
	2

zatem Odpowiedź to a = −2 lub a = −3.

Shiro: Wyznacz liczbę naturalną x: 3 * 3^x+2 = 243

psik: x ∊ N 3 * 3^x+2 = 243 3 * 3^x * 3² = 243 27 * 3^x = 243 | : 27 3^x = 9 3^x = 3² x = 2 to było proste

Shiro: Koło , kwadrat i sześciokąt foremny mają taki sam obwód równy s. Oblicz pole każdej z tych figur. Która z nich ma największe, a która najmniejsze pole.

psik: Ob_kwadratu = 4a = s Ob_koła = 2πr = s Ob_{sześciokąta} = 6b = s wszystko przedstawię za pomocą jednej zmiennej np. za pomocą 'a' 4a = 2πr | :2π

	2a
r =
	π

4a = 6b | :6

	2
b =		a
	3

Teraz tak : P_kwadratu = a²

	4a2		4a2
Pkoła = πr2 = π *		=
	π2		π

	4a2
Ponieważ π ≈ 3,14 to		≈ 1,274a2, czyli Pkoła > Pkwadratu
	π

	b2√3
Psześciokąta to 6 pól Δ równobocznych o boku b czyli 6
	4

	b2√3		4   3* a2√3   9		4		1
Psześciokąta = 6		=		=		a2√3 *		=
	4		2		3		2

	2
=		a2√3
	3

Ponieważ √3 ≈ 1,73 to: P_sz ≈ 1,14a² P_koła > P_{sześciokąta} > P_kwadratu Można też wszystko przedstawić nie za pomocą 'a' tylko np. 's', ale odpowiedź to: Pole koła jest największe.

psik: A najmniejsze jest pole kwadratu.

psik: a jeśli byś chciał za pomocą 's' to s = {a}{4}. Podstawiaj do wzorów pól i gotowe

psik:

	a
s =
	4

psik:

	s
kurcze, nie tak : a =
	4

psik: Z obwodu kwadratu że 4a =s u know what i mean

Shiro: Środki boków równoległoboku łączymy kolejno odcinkami. Jaką część pola równoległoboku stanowi pole otrzymanego czworokąta?

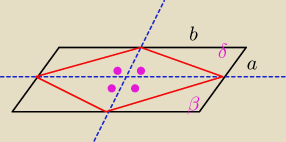
psik: Pole równoległoboku to 2a*2b*sinδ Pole czworokąta powstałego to 4 pola trójkątów, czyli 2*ab

2ab		1
	=
4absinδ		2sinδ

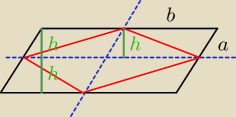
psik: Zrobimy to prościej. Tamte niebieskie proste nie padają pod kątem prostym, zrobiłem złe założenie. Pole równoległoboku to 2b*2h = 4bh Pole czworokąta to 4 pola trójkątów . Pole jednego trójkąta ze wzoru : 1/2a*h to P Δ = 1/2bh Pole czworokąta to 2bh

	2bh		1
czyli		=
	4bh		2

Odp : Pole czworokąta to połowa pola równoległoboku ( Można też po sinusach, ale wolałem nie)

Eta: @psik zad1/ dla Shiro można rozwiązać też tak: 10=(11−1) (11−1)*(11⁹ +11⁸ +11⁷+ ..... +11 + 1) +1 wykonując mnożenie otrzymujemy (11¹⁰ + 11⁹ +11⁸+ .......... +11² +11 −11⁹ −11⁸ − ......... −11² −11 −1) +1= −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− = 11¹⁰ −1 + 1= 11¹⁰

psik: Sprytnie

Eta: