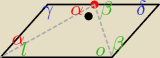
 W równoległoboku ABCD, w którym |AB| = 2|AD| punkt M jest środkiem boku CD. Wykaż że
trójkąt ABM jest prostokątny.
180−2β=δ
180−2α=γ
90(czarna kropka)= 180 − (α+β)
α+ β = 90o
l+α+o+β+δ+γ=360
l +α + o + β + 180−2β + 180−2α = 360
l − α + o − β = 0
l + o = α + β
l + o = 90o
Mogę takie coś zrobić, że od końca robie?
najpierw mowie ze tam jest kat prosty i daje wyliczenia ze l + o = 90. Innego rozwiazania do
tego zadania nie widze.
W równoległoboku ABCD, w którym |AB| = 2|AD| punkt M jest środkiem boku CD. Wykaż że
trójkąt ABM jest prostokątny.
180−2β=δ
180−2α=γ
90(czarna kropka)= 180 − (α+β)
α+ β = 90o
l+α+o+β+δ+γ=360
l +α + o + β + 180−2β + 180−2α = 360
l − α + o − β = 0
l + o = α + β
l + o = 90o
Mogę takie coś zrobić, że od końca robie?
najpierw mowie ze tam jest kat prosty i daje wyliczenia ze l + o = 90. Innego rozwiazania do
tego zadania nie widze.
 Trójkąty △ADM i △BCM są równoramienne (boki mają o długości a). Zatem kąty w trójkącie: △BMC
Trójkąty △ADM i △BCM są równoramienne (boki mają o długości a). Zatem kąty w trójkącie: △BMC
| 180o − 180o + α | α | |||
mają miarę: |∡BMC| = |∡CMB| = | = | . Podobnie rozpatrujemy kąty w | ||
| 2 | 2 |
| 180o − α | ||
drugim trójkącie: |∡AMD| = |∡DMA| = | . Teraz pozostało skorzystać z kąta | |
| 2 |
| 180o − α | α | |||
półpełnego dla trójkąta △ABM: 180o = |∡AMB| + | + | ⇒ |∡AMB| = 90o | ||
| 2 | 2 |

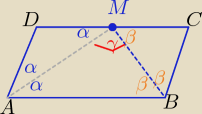 Z treści zadania wynika że trójkąty MCB i MDA są równoramienne
ponad to kąty MBA i BMC oraz BMA i AMD są kątami naprzemianległymi
z własności równoległoboku
2β+2α =180o ⇒ α+β=90o
zatem miara kąta γ= 180o −(α+β)= 90o
wniosek :Δ ABM jest prostokątny
c.n.u.
Z treści zadania wynika że trójkąty MCB i MDA są równoramienne
ponad to kąty MBA i BMC oraz BMA i AMD są kątami naprzemianległymi
z własności równoległoboku
2β+2α =180o ⇒ α+β=90o
zatem miara kąta γ= 180o −(α+β)= 90o
wniosek :Δ ABM jest prostokątny
c.n.u.


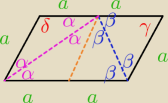 O to chodzilo?
O to chodzilo?