matura;)
Monia:
cześc ucze sie do matury i chciałabym zapytać czy za tak rozwiązane zadanie dostane max
punktów

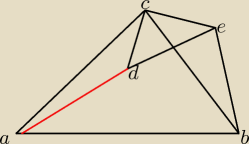
Trójkąty prostokątne równoramienne ABC i CDE są położone tak, jak na poniższym rysunku
(w obu trójkątach kąt przy wierzchołku C jest prosty). Wykaż, że |AD| = |BE| .
korzystam z cechy BBB
CB=AC
CD=CE
czyli BE=AD bo trojkąty ADC i BCE są przystające z cechy BBB
moze być tak?
6 maj 16:06
Monia: hm?
6 maj 16:18
Eta:
To nie jest poprawny dowód ( nie ma cechy przystawania (b,b)
Po drugie : wierzchołki figur oznaczamy wielkimi literami A,B,C,D, E,...
6 maj 16:20
Monia: czyli musze 3zwiazki pokazać
6 maj 16:25
Eta:
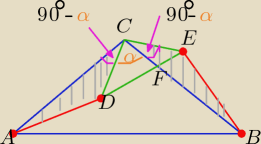
W trójkątach ADC i BCE mamy:
|AC|=|BC| i |DC|=|CE| −− z treści zadania
zauważamy,że :
|∡ADC|= 90
o−α = |∡BCE|= 90
o−α ⇒ |∡ACD|=|∡BCE| ,gdzie
α= |∡DCF|
zatem z cechy (
b,k,b ) trójkąty ADC i BCE są przystające
czyli
|AD|= |BC|
c.n.u.
6 maj 16:35
Monia: dzięki bardzo.

6 maj 16:35
Wiki: raczej |AD|= |BE|

6 maj 19:18
 cześc ucze sie do matury i chciałabym zapytać czy za tak rozwiązane zadanie dostane max
punktów
cześc ucze sie do matury i chciałabym zapytać czy za tak rozwiązane zadanie dostane max
punktów Trójkąty prostokątne równoramienne ABC i CDE są położone tak, jak na poniższym rysunku
(w obu trójkątach kąt przy wierzchołku C jest prosty). Wykaż, że |AD| = |BE| .
korzystam z cechy BBB
CB=AC
CD=CE
czyli BE=AD bo trojkąty ADC i BCE są przystające z cechy BBB
moze być tak?
Trójkąty prostokątne równoramienne ABC i CDE są położone tak, jak na poniższym rysunku
(w obu trójkątach kąt przy wierzchołku C jest prosty). Wykaż, że |AD| = |BE| .
korzystam z cechy BBB
CB=AC
CD=CE
czyli BE=AD bo trojkąty ADC i BCE są przystające z cechy BBB
moze być tak?
 W trójkątach ADC i BCE mamy:
|AC|=|BC| i |DC|=|CE| −− z treści zadania
zauważamy,że :
|∡ADC|= 90o−α = |∡BCE|= 90o−α ⇒ |∡ACD|=|∡BCE| ,gdzie α= |∡DCF|
zatem z cechy (b,k,b ) trójkąty ADC i BCE są przystające
czyli |AD|= |BC|
c.n.u.
W trójkątach ADC i BCE mamy:
|AC|=|BC| i |DC|=|CE| −− z treści zadania
zauważamy,że :
|∡ADC|= 90o−α = |∡BCE|= 90o−α ⇒ |∡ACD|=|∡BCE| ,gdzie α= |∡DCF|
zatem z cechy (b,k,b ) trójkąty ADC i BCE są przystające
czyli |AD|= |BC|
c.n.u.

