bardzo prosze o naprowadzenie:)
!!: mnej wiecej wiem jak to zrobic ale potrzebuje jednego wyjasnienia
znajdz wszystkie takie liczby rzeczywiste b aby wielomian (x
2 +bx +4 ) (x−1) miał trzy
różne pierwiastki których suma jest mniejsza od 9
wiem ze jednym rozwiazaniem jest x=1 wiec (x
2 +bx +4 ) musi miec dwa różne rozwiazania
lub dwa takie same wiec delta bedzie wieksza równa 0
dodatkowo wiem ze trzy pierwiastki maja byc mniejsze od 9
wiec ze wzoru vieta wychodzi mi ze 1 −b <9 czyli b> −8
ale w odpowiedzi pojawia sie jakas piatka jaki warunek pominelam

23 kwi 00:12
...:
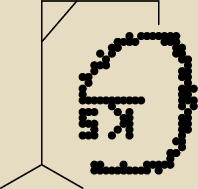
23 kwi 00:17
Basia: tylko dwa różne i na dodatek żaden nie może być równy 1 (bo mają być trzy różne
pierwiastki)
czyli pominąłeś:
x1≠1
x2≠1
23 kwi 00:18
!!: racja! dzieki

23 kwi 00:21
Bogdan:
x1 + x2 + x3 < 9
ale x1 = 1, a więc x1 + x2 < 8
dalej Δ > 0 i wzory Viete'a.
23 kwi 00:23
Eta: Podpowiadam,że rozwiązaniem równania:
x
2 +bx +4 nie moze być x= 1 ) bo pierwiastki maja być
różne
więc dla x =1 mamy:
1
2 +1*b +4 = 0 => b = 5
więc gdy x≠1 to b≠5
czyli należy odrzucić ze zbioru rozwiązań właśnie b=5
czy już jasne?....
23 kwi 00:29
Basia: Tyle, że to niczego nie zmienia, bo wychodzi b≠−5.
Czy tam przypadkiem nie powinno być x2 − bx + 4 ?
Wtedy z Δ>0 byłoby b∈(−∞,−4)u(4;+∞)
z warunku na sumę byłoby: 1 + b < 9 czyli b<8
i z x1≠1 i x2≠1 byłoby b≠5
ostatecznie byłoby: b∈(4;5)u(5;8)
23 kwi 00:30
Eta: Fakt Basia ,.....
b≠ −5 oczywiście

23 kwi 00:31



