PROblem
TOmek: rumpek, Eto help, please
Zadanie 3. (5 pkt)
Obrazem odcinka AB, gdzie A = (1, 0) i B =(2,1) w jednokładności o skali k > 1 i środku P jest
odcinek |CD|, gdzie C = (4, 0),D = (6, 2).
Zapisz równanie okręgu o środku w punkcie P i promieniu |AB| .
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Nie kminie w ogole jednokladności, nigdy tego nie miałem.
6 maj 12:10
rumpek: To to zadanie z mojej matury

?
6 maj 12:12
TOmek: ja wziąłem to zadanie z Operonu 2008 rok

6 maj 12:13
Godzio:
AP * k = PC
BP * k = PD (wektorowo)
Reszta już jasna chyba, mam nadzieję, że dobrze to pamiętam

6 maj 12:14
rumpek: Zaraz się zrobi [2009 rok]
6 maj 12:14
TOmek: zjem sniadanko i rozkminie Godziowy post

6 maj 12:14
Godzio:
Niech
rumpek najpierw potwierdzi

Z jednokładnością mam tyle wspólnego co z
prawdopodobieństwem

6 maj 12:15
Eta:
odp:
o: (x+2)
2+y
2=2

6 maj 12:17
Eta:
@
Godzio
Na tyle <jabłek> , to musisz mieć dobrą pamięć

6 maj 12:19
Eta:


6 maj 12:19
Godzio: Ufff

6 maj 12:20
Eta:
@
TOmek
Pierwszego do pomocy wymieniłeś
rumpka ........... to ja poczekam

6 maj 12:21
rumpek:
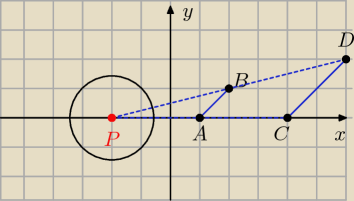
Wpierw wyznaczmy odległość między punktami:
|AB| =
√ (2 − 1)2 + (1 − 0)2 =
√1 + 1 =
√2
|CD| =
√ (6 − 4)2 + (2 − 0)2 =
√ 4 + 4 =
√8 = 2
√2
| | 2√2 | |
Zatem skala tych odcinków to: k = |
| = 2 |
| | √2 | |
Pozostało ułożyć rachunek wektorowy: P(x, y)
| ⎧ | 2 * |PA| = |PC| | |
| ⎩ | 2 * |PB| = |PD| |
|
2 * [1 − x; −y] = [4 − x, 0 − y] ⇒ [2 − 2x, −2y] = [4 − x, − y] :
1
o 2 − 2x = 4 − x ⇒
x = −2
2
o y = 0
Zatem: P(−2 , 0)
Czyli równanie tak jak podała
Eta:
(x + 2)2 + y2 = 2 
6 maj 12:26
rumpek: Kobiety mają pierwszeństwo

6 maj 12:26
6 maj 12:30
TOmek: dziekuje pieknie Wam, juz to kminie

6 maj 12:31
rumpek: Dziękować

6 maj 12:33
6 maj 12:35
Eta:
Powinieneś napisać tak:
Korzystając z rachunku wektorowego
a nie " układam rachunek wektorowy" .... ( dzieci układają zwykle klocki w przeszkolu

6 maj 12:37
Kamil: przedszkolu

6 maj 12:38
Eta:
No tak ..........w prze
dszkolu

6 maj 12:39
rumpek: 
6 maj 12:41
Eta:


6 maj 12:42
 ?
?



 Z jednokładnością mam tyle wspólnego co z
prawdopodobieństwem
Z jednokładnością mam tyle wspólnego co z
prawdopodobieństwem 






 Wpierw wyznaczmy odległość między punktami:
|AB| = √ (2 − 1)2 + (1 − 0)2 = √1 + 1 = √2
|CD| = √ (6 − 4)2 + (2 − 0)2 = √ 4 + 4 = √8 = 2√2
Wpierw wyznaczmy odległość między punktami:
|AB| = √ (2 − 1)2 + (1 − 0)2 = √1 + 1 = √2
|CD| = √ (6 − 4)2 + (2 − 0)2 = √ 4 + 4 = √8 = 2√2













