przekształcenie prosta jednokładność: Figura F₁ jest okręgiem o równaniu x²+y²+4x−2y−11=0. Okrąg ten przekształcono przez jednokładność o środku O = (1;2) i skali k = −2. Wyznacz równanie tego okręgu po przekształceniu. Chyba byłem chory kiedy w szkole była jednokładność, bo kompletnie tego nie pamiętam. Mógłby ktoś to zadanko naprawdę ładnie rozpisać? Bo znajduję podobne na necie, ale ludzie skrótami robią, np. "r₂ równe XY", bez mówienia skąd to XY. Chciałbym żeby ktoś ładnie je wytłumaczył, tak żebym zrozumiał istotę tego przekształcenia i mógł to wykorzystać do innych zadań, a nie podał czyste rozwiązanie tego zadania. Równanie okręgu F₁ po przekształceniu to: (x+2)²+(y−1)²=16, czyli S = (−2;1), r = 4 (tak dla skrócenia obliczeń). Czyli pozostaje obliczyć promień okręgu po przekształceniu (dwa, osiem, czy jeszcze inny? nie wiem czy r₁ przez r₂ czy na odwrót i czy gdzieś wartość bezwzględną czy całkiem inaczej) oraz środek S' przekształconego okręgu, podejrzewam że to (7;4), ale jednak chciałbym wszystko mieć ładnie i prawidłowo obliczone.

prosta jednokładność: tylko mi nie pomijajcie mojego wątku i pomóżcie :< to ostatnia kwestia z geometrii analitycznej, z której mam wątpliwości, chcę już to ogarnąć i przejść do następnego działu

TOmek: Ja tak samo nie ogarniam jednokładności, fajnie by było gdyby ktoś to ładnie wytlumaczył

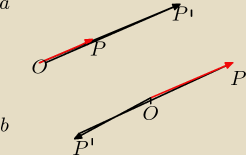
Aga1.: Musisz znać definicję jednokładności. a) k>0 b) k<0 J^k_O(P)=P^'⇔OP^'→=k*OP→

TOmek: Aga a tak bardziej na polski te zapisy pod spodem?

Aga1.: I tak O=(1,2) P=S=(−2,1), k=−2 OS→=[−2−1,1−2]=[−3,−1] k*OS→=−2*[−3,−1]=[6,2] S^'=(a,b) OS^'=[a−1,b−2] Wektory zaznaczone na niebiesko są równe,gdy a−1=6 i b−2=2 a=7,b=4 więc S^'=(7,4) r^'=IkI*r=2*4=8 Równanie okręgu (x−7)²+(y−4)²=8²

TOmek: promien w tym okręgu nie powinien mieć wartość 2

Aga1.: Skoro promień okręgu danego wynosi r=4, to r^'=IkI*r=I−2I*4=2*4=8