poziom rozszerzony
Kamil: ciekawe zadanie dla maturzystów
Trójkąt ABC jest podstawą ostrosłupa ABCS. Punkt M jest środkiem boku AB i |AM| = |MC|. Odcinek
AS jest wysokością tego ostrosłupa. Wykaż, że kąt SCB jest prosty.
6 maj 11:14
6 maj 11:16
Kamil: nie ma chętnych ?
6 maj 11:46
rumpek: Zauważ, że na podstawie można opisać okrąg
Zatem trójkąt w podstawie jest prostokątny o
wierzchołku |∡C| = 90
o, i promień okręgu to połowa |AB|
Dalej już prosto.
6 maj 12:37
Kamil: własnie to ja rozkminiłem ze mozemy sobie okrag opisac i przy wierzcholu C mamy 90
o tylko
dalej nie rozkminiam
6 maj 12:50
Kamil: mało chetnych na wykazanie , trudno
6 maj 13:10
Kamil: mało chetnych na wykazanie , trudno
6 maj 13:11
zią:
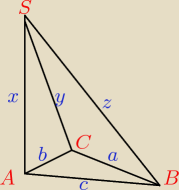
zeby wykazac ze ∡SCB jest prosty, mozesz wykorzystac twierdzenie pitagorasa
y
2 + a
2 = z
2
z tresci zadania i z tego ze podstawa jest trojkat prostokatny wynika, ze
x
2 + c
2 = z
2 oraz x
2 + b
2 = y
2
a wiec
x
2 + b
2 + a
2 = x
2 + c
2 ===> a
2 + b
2 = c
2
no i tu nalezy znac twierdzenie odwrotne do twierdzenia pitagorasa.. bo z niego wlasnie wynika
ze ∡SCB jest prosty
6 maj 13:54
Kamil: ucze sie juz tyle matmy a nie znam odwrotnego twierdzenia do pitagorasa, nie przerabialem tego
w szkole , albo mnie nie bylo
6 maj 15:58
Kamil: ale tak czy inaczej by mi te obliczenia wystarczyly, bo do tego udowodnilem ze podstawa jest
trojkatem prostokatnym
6 maj 16:00