PILNE Adam: W prawidłowym ostrosłupie czworokątnym kąt płaski przy wierzchołku jest równy α, zaś krawędź podstawy ma długość a. Oblicz promień kuli opisanej na tym ostrosłupie.

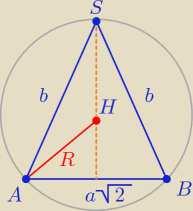
Kamil: Promień tej kuli jest taki sam jak promień okręgu opisanego na trójkącie równoramiennym, którego podstawą jest przekątna podstawy a trzeci wierzchołek wierzchołkiem ostrosłupa.

Kamil: jak juz naprawde nie bedziesz umial policzyc to Ci pomoge, moje lenistwo mnie przeraza no ale coz, narazie proboj

Kamil: oj probuj*

Adam:

	a
doszłem do czegoś takiego b=		no i za bardzo nie wiem co dalej
	2sinα2

Kamil: no i z pitagorasa wysokosc policz

Kamil:

	a√2
H2+(		)2=b2
	2

Adam: jakaś dziwna mi ta wysokość wychodzi

Adam: nie umiem jej poprawnie obliczyć

Kamil: jaka Ci wychodzi ?

Adam: coś wyszło mi

Kamil:

	a√1−2sin2α2
H=
	2sinα2

Adam:

	a√cosα
H=
	2sinα2

Adam: i teraz do wzoru

Kamil:

	a*√cosα
H=
	2sinα2

Kamil:

	abc
no pięknie , tak do wzoru P=
	4R

Adam: dziękuję

Kamil: jesli sie nie pomylilem w obliczeniach powinno wyjsc

	a		a*√cosα
R=		=
	4sinα2*√cosα		4sinα2*cosα

Adam: mi wyszło podobnie ale pojawił mi się kwadrat możesz pokazać jak liczyłeś bo gdzieś popełniłem błąd i nie mogę go znaleźć

Adam: proszę

Kamil: znalazlesc bład ?

Kamil: znalazles?

Adam: znalazłem błąd

Kamil:

	abc
R=
	4P

a=a√2

	a
b=
	2sinα2

	a
c=
	2sinα2

	a2
abc=a√2*(		)
	4sin2α2

	a√2*a√cosα		a2*√2cosα
4P=4*		=
	2*2sinα2		sinα2

rumpek: 1^o Obliczam długość boku b (ramiona ostrosłupa)

	α		a   2
sin		=		/ * b
	2		b

	α		a		α
bsin		=		/ : sin
	2		2		2

	a
b =
	α   2sin   2

2^o Obliczam wysokość ostrosłupa − H

	a√2
H2 + (		)2 = b2
	2

	a2		a2
H2 +		=
	2		α   4sin2   2

	a2		α   2a2sin2   2
H2 =		−
	α   4sin2   2		α   4sin2   2

	α   a2(1 − 2sin2 )   2
H2 =		, H > 0
	α   4sin2   2

	a√cosα
H =
	α   2sin   2

3^o Liczę pole trójkąta ACS

	1		a√cosα		a2√2cosα
P =		* a√2 *		=
	2		α   2sin   2		α   4sin   2

4^o Liczę promień opisany na trójkącie równoramiennym ACS

	abc
R =
	4P

	a2   a√2 *   4sin2( (α)/2)
R =
	a2√2cosα   sin( (α)/2)

	a3√2		α   sin   2
R =		*
	α   4sin2   2		a2√2cosα

	a
R =
	α   4sin √cosα   2

uff

Kamil: o stary, wariacik z Ciebie

Mila: 1) oblicz h_b− wysokość ściany bocznej (cotangens połowy α) 2) H −wysokość ostrosłupa z tw. Pit. 3) równanie (H−R)²+(0,5a)²=R²

Mila: 3 ) równanie ma być:(H−R)²+(0,5a√2)²=R² Wynik jak u Rumpka. Może tylko trochę mniej obliczeń.