Z parametrem RedX: Wyznacz wszystkie wartości parametru m, dla których funkcja określona wzorem f(x) = (−m³ + 9m)x + m +2 jest funkcją malejącą. Dla jakich wartości parametru m wykresem funkcji f(x) jest prosta równoległa do prostej o równaniu y = 8x − 5

Mila: f(x)=(−m³ + 9m)x + m +2 jest funkcją malejącą. f(x) −funkcja liniowa funkcja liniowa malejąca ⇔a=(−m³ + 9m)<0 rozwiąż

asdf: @Mila −m³ + 9m < 0 m(9 − m²) < 0 m(3 − m)(3 + m) < 0 jak dalej? część wspólna, czy m ∊ (−3;3) czy inaczej to będzie?

asdf: z tym (−3;3) to chyba według mnie jest źle

picia: a 0?

picia: masz 3 msc zerowe.

Mila: asdf źle, popraw, narysuj węża.(3 miejsca zerowe i zaczynasz od ..?) Redx nie rozwiązuje?

RedX: (−m³ + 9) < 0 m(−m² + 9) < 0 wg mnie dwa. m = 0 i m = 3 a druga część?

RedX: a nie. jednak 3. przepraszam

Mila: RedX nie, przeczytaj polecenie.asdf dobrze myśli, ale źle rozwiązał warunek.

Mila: b) −m³ + 9m =8

RedX: m∊ (−3;0) u (3, +∞)

asdf: Jak węże to już nie mój poziom nie czaje ich w ogóle (może dlatego, że jeszcze nigdy ich nie miałem..)

asdf: a spróbuje, tylko nie wiem czy dobrze zacząłem go rysować odp to (−∞; −3) ∪ (0;3)

picia: zaczynasz od prawej strony, patrzysz na znak przy najwyzej potedze, − to od doly ,+ to od gory. potem na krotnosc pierwiastkow. 1,3,5,7..− krotny to wezyk przechodzi, 2,4,6..krotny to odbijasz.i tyle

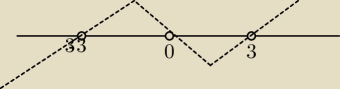
Mila: a) c,d. m(3 − m)(3 + m) < 0 ⇔m( m−3)(3 + m) > 0 m∊(−3,0)∪(3,∞)

Mila: RedX − dobrze, teraz dokończ pkt. b Wąż dla asdf.

asdf: @picia Nie rozumiem tego w ogóle... @Mila czemu (3; nieskończoności)? Twój wykres pokazuje inaczej Według mnie właśnie powinno być (−∞; −3) oraz (0;3) podkreślam W OGÓLE TEGO NIE ROZUMIEM WIĘC TO JEST PYTANIE!

asdf: b) −m³ + 9 = 8 −m³ = −1 m = 1

RedX: jak masz < 0 (tak jak w tym przykładzie) to bierzesz te co są pod osią a jak > 0 to te nad osią

Mila: asdf zauważ, że zmieniłam znak w nierówności, biorę pod uwagę wartości dodatnie, czyli nad osią.

asdf: zapomniałem o jednej nie wiadomej −m³ + 9m = 8 −m³ + 9m − 8 = 0 −m³ + m + 8m − 8 = 0 m(1 − m²) + 8(1 − m) = 0 m(1 − m)(1 + m) + 8(1 − m) = 0 (1 − m)(m² + m + 8) = 0 m = 1 oraz Δ < 0 tak?

asdf: Nie ma sensu, żebym zaczął te wężyki...bez nauczyciela nie zrozumie chyba tego, po maturze spróbuje poszerzyć swój mały zakres wiedzy..Na studia na pewno się przyda

picia: m( m−3)(3 + m) > 0 w tym przykladzie masz m³ czyli jest dodatnie czyli zaczynasz rysowanie od gory.wszystkie pierwiastki sa jednokrotne czyli wszedzie "przechodzi".

picia: a jak rozwiazesz nierownosc wielomianowa?

asdf: @Mila takie coś zrobiłaś?: m(3 − m)(3 + m) > 0 −m(3 − m)(3 + m) < 0 m(m − 3)(3 + m) < 0 Tu chodzi o to, by każda niewiadoma nie miała znaku ujemnego?

asdf: Dobra, nie będę Wam zawracać gitary, jak i tak z tego nic nie zrozumiem, było by fajnie jakby ktoś sprawdził p−pkt b)

Mila: m(3 − m)(3 + m) <0 tak było m*[(−1)(3 − m)]*(3 + m) >0⇔m(m−3)(3 + m) >0

asdf: sprawdzi ktoś post z 22⁵⁹ czy dobrze?

Mila: 3linijki dobrze, potem pomyłka.

asdf: −m³ + m + 8m − 8 = 0 m(1 − m²) − 8(1 − m) = 0 (1 − m)(m² + m − 8) = 0 m = 1 −−−−− √Δ = 5

	−1 + 5
x1 =		= 2
	2

x₂ = −3 Odp: m ∊ {−3;1; 2} git?

Mila: Δ nie zgadza się?

asdf: nom delta jest inna. "Jak się człowiek śpieszy to się diabeł cieszy"..

Mila: RedX policzył?

asdf: nie wiem ale ja chyba tej matmy nie zdam z takimi bykami

Mila: Zdasz, licz powoli i sprawdzaj z kalkulatorem. Najlepiej zapisać dokładnie według wzoru: np: Δ=b²−4ac=1¹−4*1*(−8)=1+32 pamietaj o kolejności działań, mój kuzyn jest bardzo słaby z matematyki, ale właśnie tak go nauczyłam liczyć i mam nadzieję że zda.

asdf: oby...

picia: hehe powodzenia asdf

asdf: dzieki