stereometria Gimli: WITAM! ZADANIE: Kula wpisana w stożek ma pole powierzchni dwa razy mniejsze od pola powierzchni całkowitej stożka. Oblicz cosinus kąta nachylenia tworzącej tego stożka do jego podstawy. Będę wdzięczny za liczną pomoc

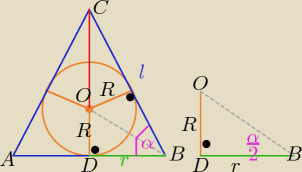Eta: R −−− dł. promienia kuli , r−−− dł. promienia stożka α € (0,90^o) z treści zad, 2*4πR²= πr(r+l) ⇒ (*) 8R²= r(r+l)

	r		r
w trójkącie DBC		= cosα ⇒ l =
	l		cosα

	R		α		α
w trójkącie DBO		= tg		⇒ R= r*tg
	r		2		2

podstawiając do wzoru (*) mamy:

	α		r2
8r2tg2		= r2+		/ : r2
	2		cosα

	α		1
8tg2		= 1+
	2		cosα

	α		cosα+1
(**) 8tg2		=
	2		cosα

	α
teraz zamieniamy tg		za pomocą cosα
	2

ze znanych tożsamości :

	α		α
1−cosα= 2sin2		i 1+cosα= 2cos2
	2		2

	α		α   2sin2   2		1−cosα
to tg2		=		=
	2		α   2cos2   2		1+cosα

wracając do równania (**) mamy:

	8*(1−cosα)		1+cosα
		=
	1+cosα		cosα

(1+cosα)²= 8cosα(1−cosα) ........ otrzymujemy: 9cos²α−6cosα+1=0

	1
(3cosα−1)2=0 ⇒ cosα=
	3

Przy okazji .........pozdrawiam Wszystkich maturzystów