g Tomek: rozwiąż nierówność log³x−logx⁴≤0 jakby ktos mogl wytłumaczyc przy okazji

Monika: Nie wiem czy to dobrze, ale cos takiego mi wyszlo: log³x−logx ≤0 log³x−4logx≤0 logx(log²x−4)≤0 logx(logx−2)(logx+2)≤0 logx * 100 * 1/100≤0 logx≤0 10⁰≤x x≥1

Eta: @Monika Po pierwsze założenie ! (bo stracisz 1pkt x>0 Dobrze "żarło i.......... " logx*(logx−2)*(logx+2)≤0

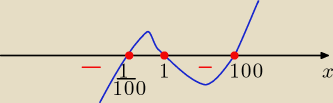
	1
miejsca zerowe x= 1 v x= 100 v x=
	100

Uwzględniając założenie, ,że x>0

	1
odp: x€(0,		> U <1,100>
	100

Monika: ok, ale nie mogę policzyć logx −2 i logx+2 tak jak to zrobiłam.. ( ze wzgledu na nierówność?)

Monika: a wynik nie powinien być x∊(1/100, 1) U (100, +∞) ?

Monika: aaa nie sory Pomylilam znak.

pigor: ... czyli jeszcze ja np. tak : (*) D=R₊ − dziedzina tej nierówności , wtedy log³x−logx⁴≤ 0 ⇔ logx(log²x−4)≤ 0 ⇔ logx(logx−2)(logx+2)≤ 0 ⇒ stąd na osi liczbowej zmiennej logx odczytujesz jej rozwiązanie : logx ≤−2 lub 0≤ logx≤ 2 , a stąd z (*) ⇔ 0< x ≤ 10⁻² lub 1≤ x ≤ 10² ⇔ ⇔ 0< x ≤¹₁₀₀ lub 1≤ x ≤100 , czyli x∊ (0;¹₁₀₀>U<1; 100> . ...

Tomek: Jestes pierwsza osoba pigor, która wytlumaczyla tak dobrze, ze nie musze sie o nic pytac Dzieki

pigor: ... no i właśnie do takich osób kieruję swoje rozwiązania, dziękuję i tak... trzymaj , pozdrawiam