
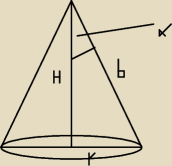
 Objętość stożka jest równa 12 π dm3, a cosinus kąta α między wysokością i tworzącą
stożka wynosi 0,8. Oblicz:
a) pole powierzchni bocznej stożka
b) miarę kąta środkowego powierzchni bocznej stożka po rozwinięciu na płaszczyźnie.
Objętość stożka jest równa 12 π dm3, a cosinus kąta α między wysokością i tworzącą
stożka wynosi 0,8. Oblicz:
a) pole powierzchni bocznej stożka
b) miarę kąta środkowego powierzchni bocznej stożka po rozwinięciu na płaszczyźnie.
| 1 | ||
V = | πr2*H | |
| 3 |
| 1 | |
πr2*H = 12π /:π /*3 | |
| 3 |
| r | ||
tgα = | ||
| H |
| 4 | ||
cosα=0,8 = | ||
| 5 |
| 16 | ||
sin2α = 1 − | ||
| 25 |
| 9 | ||
sin2α = | ||
| 25 |
| 3 | ||
sinα= | ||
| 5 |
| sinα | 35 | 3 | 5 | 3 | ||||||
tgα = | = | = | * | = | ||||||
| cosα | 45 | 5 | 4 | 4 |
| r | 3 | ||
= | |||
| H | 4 |
| 4 | ||
H = | r | |
| 3 |
| 4 | ||
r2* | r = 36 /*3 /:4 | |
| 3 |
| 3*36 | ||
r3 = | = 3*9 = 27 | |
| 4 |
| r | ||
sinα = | ||
| b |
| r | 3 | 15 | ||||
b = | = | = | ||||
| sinα | 35 | 3 |
| Pkoła | 360 | ||
= | |||
| Pb | β |
| 25π | 360 | ||
= | |||
| 203π | β |
| 3 | 360 | |||
25* | = | |||
| 20 | β |
| 3 | 360 | |||
5* | = | |||
| 4 | β |
| 15 | 360 | ||
= | |||
| 4 | β |
| 4*360 | 4*120 | |||
β = | = | = 4*24 = 96 | ||
| 15 | 5 |