planimetria pp: Trókąt SBC jest wpisany w okrąg o środku O. Wiadomo, że |kątBAC| =70stopni, |katAOB|=100stopni. Wówczas: kąt ABC równa się?

krecik:

Ajtek: Kto to kopie A może dla krecika

Michał: juz pomagam

krecik:

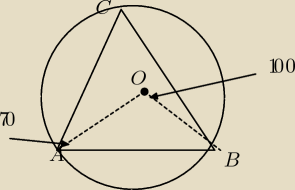
Michał: Jeśli AOB ma 100st to ACB ma 50 (kąty na tym samym łuku i mamy wpisany i środkowy) Dalej jesli AOB to 100 st i odc AO i OB to promienie to mamy trójkąt równoramienny więc kąty przy jego podstawie mają po 80:2= 40 stopni. Czyli CAO ma 30 bo CAB ma 70. Na koniec suma miar kątów to 180 st więc 180−70−50=60 st. wiec ABC ma 60 st. Wiec nawet nie trzeba było kożystać z trójkąta AOB

krecik: korzystać