Dowód Ota: Udowodnij, że jeżeli a>0, b>0, c>0 oraz a+b+c=1, to: ¹_a+¹_b+¹_c≥9

Ota: Pomoże ktoś?

Godzio:

a + b + c		3
	≥		(ŚA ≥ ŚH)
3		1   1   1   + + a   b   c

1		1		1
	+		+		≥ 9
a		b		c

Ota: Niestety ale chyba nie bardzo rozumiem skąd to się wzięło?

blogther: co to jest ta srednia harmoniczna drugi raz cos takiego widze i to drugi raz przy tym zadaniu jest jeszcze jakis prostszy ale to prostszy sposob na rozwiazanie tego zadania?

Eta: 2 sposób:

	a		b
z nierówności :		+		≥2
	b		a

1

1

1

1

1

1

1(

+

+

) = (a+b+c)*(

+

+

)=

a

b

c

a

b

c

b

c

a

c

a

b

= 1+

+

+

+1+

+

+

+1=

a

a

b

b

c

c

a

b

c

a

c

b

= 3 +(

+

)+(

+

)+ (

+

)≥3+2+2+2 =9

b

a

a

c

b

c

blogther: a skad otrzymujemy taka nierownosc ^a_b + ^b_a ≥ 2

blogther: jak widze rozwiazanie jest duzo łatwiejsze ale nie wiem skad sie to bierze

Eta:

	a		b
Wykazuję ,że		+		≥2
	b		a

b²+a²≥2ab a²−2ab+b²≥0 (a−b)²≥0 c.n.u

Eta: Wiedziałam,że o to zapytasz

Eta: Łatwiejszy jest dowód podany przez Godzia

blogther: mam podobne zadanie i tez nie moge sobie z nim poradzic na pierwszy rzut oka wyglada to na zastosowanie wzorow skroconego mnozenia zaraz napisze tylko poczekajcie okey

blogther: no tak wle co to jest ta srednia harmoniczna to jest moje drugie spodkanie z tym pojeciem

blogther: liczby nie zerowe a b c spełnija warunek a³ + b³ = 2c³

1		1		2
	+		=
a2 +ac + c2		c2 +cb + b2		a2 +ab + b2

Eta: http://docs9.chomikuj.pl/382434851,0,0,Nier%C3%B3wno%C5%9Bci-mi%C4%99dzy-%C5%9Brednimi-liczbowym-i-ich-zastosowanie.doc

blogther:

1		1		2
	+		=
a2 +ac + c2		c2 +cb + b2		a2 +ab + b2

pierwsze co zrobiłem to

a−c		c−b		2(a−b)
	+		=
(a−c)(a2 +ac + c2)		(c−b)(c2 +cb + b2)		(a−b)(a2 +ab + b2)

a−c		c−b		2(a−b)
	+		=		co dalej i czy potrzebnie to zrobiłem?
a3−c3		c3−b3		a3−b3

blogther: nie prosze o rozwiazanie tylko o podpowiedz co dalej

pigor: ... ale z założenia masz : a³+b³=2c³ ⇔ a³−c³ = c³−b³ , więc .dalej ..

Eta: a³+b³=2c³ ⇒ a³−c³= c³−b³

blogther: czyli co

2(a −c)		2(a −b)
	=
2(a3 −c3)		2c3

(a −c)		(a −b)
	=
(a3 −c3)		c3

Eta: Dodatkowo z założenia a³−b³= 2c³−2b³ ⇒ a³−b³= 2(c³−b³)

	a3−b3
to c3−b3=
	2

teraz już z górki

Eta: Nie tak

a−c		c−b		a−b		a−b
	+		=		=		=..........
c3−b3		c3−b3		c3−b3		a3−b3   2

blogther: w tych zadaniach jest za duzo dopisywania roznych rzeczy ja za takimi zadaniami nie przepadam ale nie zabardzo widze Eta gdzie ja miłbym zastosowac twoje przekształcenia do moich wyliczen

blogther: nic z tego nie bedzie jak takie zadanie na maturze bedzie to od razu albo pomine albo wykonam tylko tej operacje ktore bede potrafił

Eta: To są łatwe dowody, trzeba tylko nieco potrenować

blogther: jutro sie tym zajme od rumpka mam jakos strone z tego typu zadaniami mam jeszcze takie zadanie

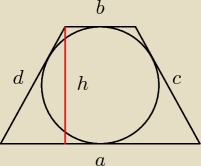
blogther: Trapez równoramienny jest opisany na okręgu. Suma długości krótszej podstawy i ramienia trapezu jest równa 30. Wyraź pole tego trapezu jako funkcję długości jego ramienia. Wyznacz dziedzinę tej funkcji.

blogther:

blogther: d + c = a + b b + d = 30 nie umiem wyznaczyc tutaj wysokosci w pitagorasa chyba trzeba to policzyc ale nie wiem jak zapisac ten krotki bok na podstawie a

blogther: nie mam pojecia jak ugrusc to zadanie

kylo1303: Pamietaj ze to trapez rownoramienny, bo widze ze wprowadziles 2 niewiadome na ramionach.

blogther: a + b = 2c własnie w podpowiedzi do zadanie było to napisane i sie dziwiłem skad sie to wzieło

blogther: dobra dzieki za pomoc jutro sie to tego zadania zabiore dobranoc

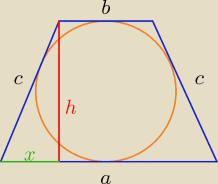
Eta: b+c=30 ⇒ c= 30−b i a+b= 2c ⇒ a= 2c−b = 3c−30

	a−b
x=		= ...... = 2c −30
	2

h²= c²−x² =......... dokończ

Eta: Z warunku opisania trapezu na okręgu ( suma długości a+b = c+c)

pigor: ... np. tak : b+r=30 i b+a=2r ⇒ b=30−r i a=2r−b=2r−30+r=3r−30 , oraz h² = r²− (¹₂(a−b))² = h²=r²−¹₄(4r−60)² = r²−4(r−15)² = = (r−2r+30)(r+2r−30) = −3(r−30)(r−10) ⇒ h=√−3(r−30)(r−10) , więc P(r) = ¹₂(a+b)h = ¹₂*2r √−3(r−30)(r−10) = r √−3(r−30)(r−10) , gdzie r∊(10; 30)=D − szukana dziedzina funkcji P . ...

Eta: No i pigor się "wychylił" i finał

blogther: no nie wiedziałem własnie jak zapisac ta długosc x

kylo1303: pigor Tak na przyszlos to blogther jest uzytkownikiem naprawde ambitnym i stara sie sam robic zadania, takze lepiej by bylo jakby ograniczyc sie do podpowiedzi, naprowadzenia na dobry tok rozumowania. Pozdrawiam.

Eta: @pigor ........ co oznaczyłeś przez "r" ? Kolizja oznaczeń ( r − dł. promienia )

blogther: probowałem jakos tak ze to a = b + 2x no to x = a − b − x a ty to po prostu podzieliłas przez dwa teraz dopiero to zauwazyłem

pigor: ... przepraszam, ale sprawdźcie, czy gdzieś sie nie kopnąłem , bo ... było szybko i online tak już też na dobranoc ...

Eta:

	a−b
W każdym trapezie równoramiennym x=
	2

pigor: ... moje r to ramię trapezu , czyli twoje c , też przepraszam, ale jak pisałem, nie widziałem twojego rysunku

blogther: dziedzina to (15;30)

Eta: Zwykle, jeżeli jest mowa o okręgu , to ramię oznaczamy inną literką, właśnie po to by nie wprowadzać kolizji oznaczeń

pigor: ..., do kylo1303 hmm... , ja widzę nawet jego jej przerost (czytaj − brak pokory), dlatego wydaje mi się , że nie zaszkodzi mu podrzucić ... co nieco , bo przy moich rozwiązaniach trzeba poruszać głową , a ze swoimi rozwiązaniami, może się on po prostu na maturze ... nie wyrobić w czasie . ...

kylo1303: No tez prawda, jesli chodzi o podawanie pelnych rozwiazan to jedni przeanalizuja i sie czegos naucza, ale sa tez tacy co przepisa do zeszyciku i uznaja za zrobione Ja juz lece spac, dobranoc wszystkim.

yhym:

1		1		1		9
	+		+		=
a		b		c		a+b+c

Da ktoś wynik z objaśnieniem?

PW: To co napisał Godzio: nierówność między średnią arytmetyczną a harmoniczną. Twierdzenie to mówi jeszcze kiedy ma miejsce równość − wtedy i tylko wtedy, gdy składniki są równe, w tym wypadku a=b=c

pigor: ..., na pewno wszystko napisała(e)ś ?, np. gdzie masz jakieś założenie napisz ""toto" porządnie w nowym temacie (poscie), bo ja np. nie mam zamiaru się domyślać o co ci (autorowi) chodzi . ...