układ równań z parametrami gorzy: Rozwiąż graficznie układ równań: y = |x−3| − 1 i w układzie mam: |x| + |y| = 4 Ładnie proszę o pomoc

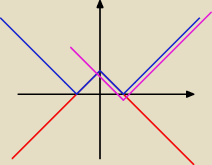
Maslanek: Ta spoko xD Jeśli się nie mylę z własnym wykresem, to: x=−1... Ale to na prawdę nie jest najlepszy pomysł temu wierzyć

Basiek: http://www.wolframalpha.com/input/?i=plot++y+%3D+%7Cx%E2%88%923%7C+%E2%88%92+1+and+plot+++%7Cx%7C+%2B+%7Cy%7C+%3D+4+ Pierwszy jest chyba banalny. Drugie równanie zawsze opisuje jakiś czworobok, najczęściej romb (chyba zdarzył mi się też raz kwadrat). To drugie raczej należy zrobić "łopatologicznie", czyli po prostu przedziałami....

Maslanek: Czyli jednak jesteś baranem

Basiek: Że ja?

Maslanek: Oj... Ja Wybacz

Basiek: Hahaha. "Bawisz mnie"− jak to pewna osoba powiedziała. Oj, Maslanek− mówią, że głodnemu chleb na myśli.

Maslanek: To moje słowa?

Basiek: O ile mnie pamięć nie myli. Nie przejmuj się, to zdaje się pierwszy Twój błąd jaki widzę Aż nie mogłam uwierzyć wolframowi, że mówi coś innego

Mila: |x|+|y|=4 kwadrat o wierzchołkach: (4,0),(−4,0),(0,4)(0,−4)

Maslanek: Idę pogrążyć się w nicość... Jak coś to zapukaj trzy razy i przytupnij nóżką...

Basiek: Nie mogę tupnąć nóżką w nicość. (A pogrążenie się w nicość to chyba współcześnie u facetów: "Idę sobie pograć") http://www.wolframalpha.com/input/?i=%7Cx%7C%2B%7Cy%7C%3D4 Muszę tę funkcję jeszcze ogarnąć do końca.

Maslanek: Akurat idę pobawić się pochodnymi... Ale to też mi nie wychodzi, bo jest jakieś dziwne zadanie, którym się zapewne podzielę... Więc chyba masz rację i pogrążę się w czarną dziurę To zadzwoń jak nie możesz tupnąć.

Basiek: Zadzwonić nie mogę tym bardziej. Ale jeśli pochodne sprawiają Ci... (jej, to dziwne) radochę, to idź Mila− mogę zapytać o coś związanego z tą funkcją?

Mila: Basiek, proszę bardzo.

krystek: Rozpatrzyć 4 przypadki 1)x≥0 i y≥0 wtedy x+y=4⇒y=−x+4 2)x≥0 i y<0 wtedy x−y=4⇒y=x−4 3)x<0 iy≥0 4)x<0 i y<0

Basiek: O, super (1) |x−6|+|y−6|=10 (to nadal będzie kwadrat? O miejscu przecięcia przekątnych (6,6)?) I tak samo inne, tym podobne?

Basiek: (2) czy np. |x−2|+|y−4|=5 nadal opisuje kwadrat ? Ogólnie... trochę tej jednej funkcji nie rozumiem do końca.

krystek: musisz analogicznie rozpatrywać 1)x≥2 i y≥4 itd j.w.

Basiek: Ja wiem, Krystek, na maturze z pewnością nie mogę sobie napisać, że tak zwyczajnie jest. Chodzi mi raczej o to, że ja zawsze jakiś głupi błąd zrobię w obliczaniach, jeśli będę mieć coś takiego, chciałabym na wstępie wiedzieć mniej−więcej co powinno mi wyjść na końcu.

gorzy: okok, czyli zapisuje na wykresie osobno oba wykresy? jak mam zaznaczyć ich rozwiązanie, tej pierwszej części i drugiej?

Basiek: Miejsca przecięcia to Twoje rozwiązania

gorzy: Dziękuję

Mila: Basiek, trzeba rozpisać. We wszystkich arkuszach Pazdro(które mam) tylko jeden układ był, równania podobne do do tego co podał "gorzy'. Nie będzie źle.

Mila: gorzy − podaj rozwiązania, poprawiłes I wykres?

Basiek: Rozpiszę, rozpiszę. Ja się wręcz modlę o funkcje Tylko ciekawi mnie sposób powstawania tej właśnie, a nie mam pojęcia, jak to w wyszukiwarkę wpisać

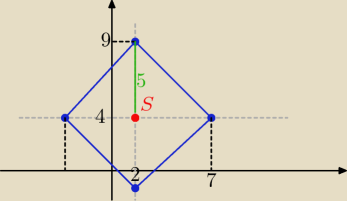
Eta: S(0,0) przesuwasz o wektor [2,4] i malujesz kwadrat

Basiek: *−*

Eta: Namaluj |x+2|+ |y−1|= 3

Eta: Ale bez pomocy wolframa

Mila: Eto, zepsułaś zabawę. Wszystko podajesz na tacy. Pozdrowienia.

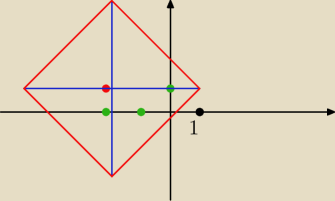
Basiek: czerwona kropa(−2,1)

Eta: @Mila ......... nie wiem o co Ci chodzi? Często widzę podawane przez Ciebie rozwiązania ......... nawet na "złotej tacy" Pozdrawiam

Eta: No i gitara

Eta: Ten ostatni komentarz → do Basiek

Basiek: Przyznaję, że na ten fakt nie narzekam.

Eta:

Basiek: Dziękuję Wam obu, naprawdę kochane jesteście. Myślę, że nie tylko mnie jednej (nie raz zresztą) uratowałyście tyłek, no i (a może tym bardziej) udowadniacie, że matematyka może być prosta i przyjemna.

Eta: Dzięki Idę się odstresować ( dobrą herbatką

krystek: @Eta Ty stresy ?