matura Kasia: Powtóka − Matura 2012 Witajcie matura z matematyki zbiża się wielkimi krokami i wpadłam na pomysł żeby zrobić grupową powtórkę, co Wy na to? mówię tu o poziomie PODSTAWOWYM. Reszte odsyłam do innych postów ktoś zarzuci jakimś zadankiem?

Kasia: oczywiście miała być powtóRka w nagłówku, ale nie wyszło..

Henio: W trójkącie ABC dane są boki o długości a i b. Znajdź długość boku c wiedząc, że suma wysokości poprowadzonych do boków długości a i b jest równa trzeciej wysokości.

kacper: Jasne, że tak. Wszyscy święci ubolewają nad moją wiedzą matematyczną ^^ U mnie będzie walka o 30%

kacper: Henio bardziej podstawowe zadania

Henio: kacper to coś dla ciebie http://www.irek.edu.pl/matura/porady/porada_18.pdf

Henio: hmm zaraz coś poszukam bez dowodzenia

ola: na zadaniainfo.pl jest dużo arkuszy

ola: zadania.info.pl − poprawka

Kasia: ee, Henio, a to do podstawy się na pewno zalicza?

kacper: Przeczytałem ten plik .pdf Dzięki

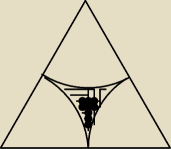
Henio: Trójkąt przedstawiony na rysunku jest trójkątem równobocznym o boku długości a. Oblicz pole zacienionej figury (powstałej po odjęciu od trójkąta kół o środkach w wierzchołkach trójkąta i promieniu długości 1/2a) Zacieniowana figura to te majtki.

Arcane ShadowMaster: Proponuję rozwiązać arkusz próbnej matury z gazetą wyborczą ta co się ukazała w kwietniu jeśli nie robiłaś, ja liczę z matmy na 90−100%, a robiąc tą miałem spore problemy z niektórymi zadaniami, osiągnąłem ok. 60%, więc chyba warto przećwiczyć ten arkusz.

Kasia: bardzo śmieszne, pisałam wyraźnie o PODSTAWOWEJ maturze..

Henio: To na dowodzenie polega tylko na wykorzystaniu jednego wzoru: PΔ=1/2ah

fanaberia: Ja mam pełno zbiorów z chomika. Poszukaj tam.

Kasia: hm, a jest gdzieś może ten arkusz dostępny? z chęcią rozwiąże

kacper: Ja rozwiązywałem arkusz z wyborczej i poszedł mi delikatnie mówiąc tragicznie

Arcane ShadowMaster: Czekaj, poszukam.

Henio: To ja już niewiem co jest podstawowe. W tym zadaniu z majtkami trzeba tylko obliczyć pole trójkata której jest równe a√3/4 i od niego odjąć połowe pola koła o promieniu 1/2a i tyle.

fanaberia: Henio: oblicz pole całego trójkąta i odejmij od tego 3 wycinki koła

Arcane ShadowMaster: To to http://www.edulandia.pl/matura/1,118553,11599097,Probny_egzamin_maturalny_z_Gazeta_Wyborcza___matematyka_.html.

Kasia: ok, dzięki Arcane

Henio: Dobra to jest napewno podstawowe macie: Bok rombu ma długość równą 5 a suma długości jego przekątnych jest równa 14. Oblicz długość wysokości tego rombu.

Kasia: strona nie została znaleziona... : ((

Henio: Te 3 wycinki to wlasnie połowa koła

Arcane ShadowMaster: A teraz? http://www.edulandia.pl/matura/1,118553,11599097,Probny_egzamin_maturalny_z_Gazeta_Wyborcza___matematyka_.html

Kasia: hula dzięki! to idę rozwiązywać i zaglądne tutaj później

kacper: Jak zrobić to zadanie Henio? Od czego zacząć?

Arcane ShadowMaster: Ok.

Dżoli: no własnie wie ktoś gdzie jest ten arkusz z wyborczej dostępny? też z chęcią bym go rozwiązała...

Arcane ShadowMaster: http://www.edulandia.pl/matura/1,118553,11599097,Probny_egzamin_maturalny_z_Gazeta_Wyborcza___matematyka_.html Tu

Arcane ShadowMaster: Kacper skorzystaj z tego że przekątne rombu dzielą się na połowy.

Dżoli: aaa, macie strony podane xD sorka, nie odświeżyłam strony i nie widziałam późniejszych wpisów

Arcane ShadowMaster: Luuz.

Henio: Możecie skorzystać sobie z tej strony: http://www.irek.edu.pl/indexx.php?id=matura Wszystkie matury od 2005 roku + kilka dodatkowych zestawów.

kylo1303: Zeby sprawdzic jaka to czesc kolo zwroc uwage na katy

fanaberia: Wykaż że jeśli α jest kątem ostrym, że sinα<1/2 to cos²α*tg²α−cos²α <−1/2

jarke: @ Henio, przyda się, dzięki

Isme: Zadania wykaż że... albo udowodnij... są najgorsze i zupełnie nie wiem o co w nich chodzi .

rumpek:

	1
cos2x * tg2x − cos2x < −
	2

	sin2x		1
cos2x *		− cos2x < −
	cos2x		2

	1
sin2x − cos2x < −
	2

	1
sin2x − 1 + sin2x < −
	2

2sin²x < 0,5 − 1

	1
sin2x <
	4

	1		1
sinx <		∨ sinx > −		z tezy jednak wiemy, że tylko 1 opcja
	2		2

c.n.u.

Isme: http://www.tomaszgrebski.pl/viewpage.php?page_id=13 tu też jest kilka matur, najbardziej kłopotliwe dla mnie są matury z PAZDRO.

fanaberia: My jesteśmy klasą rozszerzoną a nauczyciel powiedział, żeby kupować podstawy z Pazdro bo ociera się mocno o rozszerzenie, więc jeśli zdajesz podstawę to bym się nie martwiła

jarke: ma ktoś może jakieś zadania z geometri/planimetrii na wykaż że, udowodnij z podstawy? mam z nimi spory problem, a zazwyczaj jest jedno na podstawie... chętnie bym zrobił, ale to jutro, dzisiaj święto z góry bardzo dziękuję

Kasia: haha, też musiałam rozwiązywać arkusze z Pazdro, i fakt faktem dużo zadań trudnych otwartych, ale lepiej robić trudniejsze i później nie mieć problemu z łatwymi niż na odwrót ; )

rumpek: Jakieś zadania wykaż, że z podstawy mogę wrzucić

Kasia: też bym poprosiła, ale to na później bo teraz robie jeszcze arkusz z wyborczej

asdf: rumpek, będę wdzięczny

asdf: Jak ktoś chce to mogę podesłać kilka zadań z książki Pazdro (zakres podstawowy) za 6 punktów, tylko najlepiej podać dział, bo nie chce mi się wszystkiego przepisywać

Isme: Wykaż że skoro k, n ∊ N oraz n ≥ k ≥ 2, to k(n−k+2) ≥ 2

Isme: tam powinno być ≥2n . przepraszam

asdf: Stereometria: 1) Miary kątów pewnego trójkąta prostokątnego tworzą ciąg arytmetyczny. Trójkąt obraca się najpierw wokół krótszej przyprostokątnej, a potem wokół dłuższej; powstają dwie bryły o objętości odpowiednio V₁ i V₂. Wykaż, że V₁ : V₂ = √3 Planimetria: Czy istnieje parametr k e R, dla którego wierzchołkiem paraboli o równaniu y = x² − 8x + 14 jest środek okręgu o równaniu x² + y² + 4kx − 2ky + 5k² = 0? Odpowiedź uzasadnij.

rumpek: co tu udowadniać ? k(n − k + 2) ≥ 2n kn − k² + 2k ≥ 2n −k² + 2k + kn − 2n ≥ 0 −k(k − 2) + n(k − 2) ≥ 0 (−k + n)(k − 2) ≥ 0 No i teraz mamy k − 2 ≥ 0 ⇒ k ≥ 2 oraz −k + n ≥ 0 ⇒ n ≥k Zatem faktycznie: n ≥ k ≥ 2 c.n.u.

asdf: Wykaż, że skoro k,n ∊ N oraz n ≥ k ≥ 2n, to k(n − k + 2) ≥ 2n Takie coś?

Isme: hahaha No nie wiem takie zadanie z podstawy dałam. asdf tak tak takie coś

rumpek: x² + y² + 4kx − 2ky + 5k² = 0 (x² + 4kx + 4k²) − 4k² + (y² − 2ky + k²) − k² + 5k² = 0 (x + 2k)² + (y − k)² = 0 Nie, ponieważ promień nie istnienie, także to nie jest okrąg c.n.u. [sprawdzić trzeba obliczenia]

asdf: rumpek zarzuć tymi zadaniami

rumpek: Zad 1 z tymi "stożkami" robiłem już na forum gdzieś Albo na innym forum

rumpek: jutro

Maslanek: x_w = 4 y_w = −2 (x+2k)² − 4k² + (y−k)² − k² + 5k² = (x+2k)² + (y−k)² = 0 Z technicznego widzenia to punkt, więc teoretycznie nie... Ale jeśli może być to też punkt, to: 4=−2k oraz k=−2 => k=−2

asdf: Jak ktoś chce, to niech robi Ja spadam: Trygonometria: Oblicz miarę kąta ostrego x, jeśli wiadomo, że liczby: sinx, √3tgx, 3sinx, w podanej kolejności, są wyrazami ciągu arytmetycznego. Wyznacz różnicę tego ciągu.

fanaberia: Funkcja kwadratowa f ma następujące własności: – zbiorem wartości funkcji f jest przedział (–∞, 8;> – funkcja f jest rosnąca w przedziale (–∞, 3) i malej¹ca w przedziale <3, +∞); – wykres funkcji f przecina oś OY w punkcie, którego rzędna jest równa (–10). Wyznacz wzór funkcji f w postaci iloczynowej.

rumpek: 2√3tgx = 4sinx / : 2 √3tgx = 2sinx

√3sinx
	= 2sinx / * cosx
cosx

√3sinx = 2sinxcosx 2sinxcosx − √3sinx = 0 sinx(2coxs − √3) = 0 Dalej wiadomo

Maslanek: 2p{3] tgx = 4sinx

	sinx
√3 *		= 2sinx
	cosx

√3 = 2cosx

	√3
cos x =		⇒ x=30o.
	2

asdf: Z tą funkcją zadanie: y = a(x − 3)² + 8 f(0) = −10 −10 = 9a + 8 a = −2 y = −2(x − 3)² + 8 teraz zamienić na postać ogólną, później pierwiastki i na postać iloczynową.

fanaberia: a skąd się wzięła 1 linijka bo nie łapię

Maslanek: Masz tam podane współrzędne wierzchołka paraboli, tylko trochę ukryte

asdf: postać kanoniczna: y = a(x − p)² + q q = 8 (zbiór wartości funkcji jest o −∞; 8) p = oś symetrii paraboli więc określa początek i koniec przedziałów monotoniczności = 3

fanaberia: dziękuję bardzo

jarke: @Rumpek, będę bardzo wdzięczny, zobowiązuję się do rozwiązania wszystkich aczkolwiek będzie ciężko ^^ około 14, 15 powinienem się pojawić

jarke: rumpek, jak znajdziesz czas to wrzuć te zadania na udowodnij, wykaż że z geometrii/planimetrii z podstawy

kacper: Może jakieś zadanie proste ktoś wstawi

Kasia: również jestem chętna

Isme: Właśnie robię maturki więc prosze : Oblicz pole rombu ABCD wiedzac, ze A = (−3, 4) , B = (1, 2) , C = (5, 8).

Natalia:

	cos40
Wartość wyrażenia		wynosi:
	cos50

A.1

	1
B.
	2

C.tg50 D.cos50

kacper: Nie ogarniam.

Isme: wiem, że trzeba skorzystać z : sin (90* − α) = cos α ale nie za bardzo mi chyba wychodzi..

Kasia: Isme, wystarczy wyznaczyc odleglosc miedzy dowolnymi dwoma puntami. Nastepnie wyznaczamy prosta przechodzaca przez powiedzmy punkty A i B, tworzymy do niej prostopadla ( w celu wyznaczenia dlugosci wysokosci) i.. teraz mam mały dylemat, bo potrzeba wysokosci, wyznaczyloby sie dlugosc korzystac np. z punktu C i potrzebny jest jeszcze jakis punkt na odcinku AB.. eee niech ktos ratuje

Kasia: co do zadania z cos, nie wystarczy podstawic wartosci z tablic? i po sprawie, nie trzeba znac zadnych zaleznosci i kombinowac

Basiek: Isme− ja chcę zrobić Mogę?

Kasia: podejrzewam dodatkowo,ze Natalia zle przepisala zadania.. gdzies zamian cos jest pewnie sin. wtedy sie piekne przeksztalca na ten sam cos i wychodzi 1

Kasia: zadanie*

Kasia: Basiek, zrób to z rombem

Basiek: wektory: AB= [4, −2] AC=[8, 4] | 4 −2|

	1
2PΔ{ABC}=Prombu= 2*		| d(AB, AC)|= | 8 4| = 16+ 16= 32
	2

Mam nadzieję, ze jest dobrze

Basiek: Analityczna

Isme: A to dobrze mi wyszło bo wyszło mi 1 ale jakoś nie byłam pewna . Do tego rombu nie mam odpowiedzi więc Wam niestety nie powiem czy dobrze... Ale wyszło m itak jak Tobie Basiek

Isme: Mam kilka zadanek z odp A,B,C,D mogę podawać jak ktoś chętny,.

Kasia: wrzucaj, wrzucaj

Basiek: Ja do sprzątania, a potem do nauki. W końcu trzeba dotknąć książek. Mam ostatnio taki specyficzny wstręt do nich A Wy się tu dalej bawcie. Zadanko fajne, tylko trochę za proste

kacper: Poproszę o nie

kacper: Basiek zdolna jesteś, znajdziesz sobie trudniejsze

Isme: [P[Basiek] Zadanka proste, ale na podstawę starcza . Miłego sprzatania, a i uwierz ja też mam wstręt do książek . Zaraz coś wam podam − tylko znajdę jakieś fajne

Kasia: ja też mam wstręt do książek, przez ostatni tydzień około 20 lektur latały ze mną po domku i mam dość za to zadanka z majcy z wielką chęcią porobie czekam cierpliwie

Isme:

	1
Rozwiązaniem równania :		x + log2 8 = 3x − 2
	2

A) x = 8 B) x = 0 C) x = −2 D) x = 2

Basiek: Znajdę, potem. Zdolna może i nie jestem, ale analityczna to mój ulubiony dział. A na podstawę.... jak najbardziej. Skąd bierzesz zadanka Isme? [I takie pytanie− trochę nie na temat: nie wie ktoś, gdzie można znaleźć jakieś fajne readingi na poz. rozsz? Poszukuję, znaleźć nie mogę]

Isme: Prosta o równaniu √3x − 3y +12 = 0 jest nachylona do osi OX pod katem A) 45° B) 30° C) 54° D) 60°

kacper: To jest to fajne zadanko

Basiek:

x
	+3=3x−2
2

x−6x=−4+6 −5x=10 => x=−2 ? C

Isme: Wiesz co ja najcześciej ściągam sobie wszystko z chomikuj.pl bo mam dość duży transfer wiec się mogę pobawić w rożne ściągania repetytorium czy inne takie . Co do angielskiego, dziś wieczorem będę czegoś szukać bo sama muszę w końcu angielski zaczać ćwiczyć wiec jak coś znajdę to się pochwalę Tobie Basiek

Kasia: Basiek! idz sprzatac, a nie bierzesz sie za zadania z podstawy

Kasia: Isme, gdybys miala jakies watpliwosci co do angielskiego, to służę pomocą

Basiek:

	√3
y=		x+4
	3

a=tg30 (B) Ej, ja nic nie mówię, ale ostatnie próbne z CKE napisałam na 70% Więc wiecie...

Kasia: jedna wpadka na sto to wiesz.. na prawdziwej i tak będziesz miała 100%, no w ostatecznosc 99

Basiek: Jeśli chodzi o 99%, to ogólnie nie ma takiej możliwości Wiesz, jedna wpadka..., tylko to właśnie jest "zue" w maturach. Jeden gorszy dzień, jeden głupi błąd, ....

kacper: Nie można mieć 99% z matmy podst. może być 98% tylko parzyste

Kasia: ale łapiecie za słówka, a raczej za liczby.. no niech Wam będzie, 98 no tak jest, ale każdy przez to musi przejść, to chyba pociesza. Nie każdy może dać z siebie 100% w każdy z tych dni..

Basiek: Kiedyś czepiałam się słówek, od pewnego czasu... liczb. Ogólnie, straszne pranie mózgu . Zarzucam matematycznym sucharkiem: http://matematyczny.blox.pl/2008/09/Skad-sie-biora-dzieci.html I znikam (teraz już serio− serio) Gdybyś coś Isme wychomikowała, to trzymam słowo, że dasz znać.

Isme: http://www.cke.edu.pl/images/stories/009_matem_proba/091208_zasady_punktowania.pdf Może warto zajrzeć?

kacper: Zajrzałem

jarke: up

asdf:

	cos40ox
Wartość wyrażenia
	cos50ox

wynosi: A.1

	1
B.
	2

C.tg50 D.cos50 Tu nie powinno być: ctg50^o albo tg40^o

Basiek:

cos(90−40)		sin50
	=		=tg50
cos50		cos50

mala2: @ Henio zadanie "z majtkami" katy trójkąta równobocznego To są 3 wycinki koła, kazdy o kacie środkowym 60 stopni 3*60=180 stopni korzystam z równości α360 = Pwπ r2 , gdzie Pw to pole wycinka 180360 = Pwπ r2