gf blogther:

	1
Wiadomo, że liczba a jest rozwiązaniem równania		+ x = 5, gdzie x ≠ 0. Nie wyznaczając
	x

	1
a, oblicz wartość wyrażenia		+ a3.
	a3

Aga1.:

	1
(		+a)3=53
	a

	1
Zastosuj wzór skróconego mnożenia i wykorzystaj, że		+a=5
	a

Eta:

1		1		1
	+a3= (		+a)3−3(		+a)=...
a3		a		a

blogther: mam pytanie dlaczego zapisujecie to ten sposob

1		1
	+ a3 = (		+ a)3
a3		a

nie powinno byc

	1		1		1		1
(		)3 + a3 = (		+ a)(		−		*a + a2)
	a		a		a2		a

blogther: a³ * b³ = (ab)³ to zgoda ale nie a³ + b³ ≠ (ab)³

Eta: Ze wzoru na sześcian różnicy (a+b)³= a³ +3a²b+3ab²+b³ to a³+b³ = (a+b)³ −3a²b−3ab²

Eta:

1		1		1		1		1		1
	+a3=(		+a)3−3*		*a −3*		*a2=(		+a)3−3(		+a)
a3		a		a2		a		a		a

Aga1.: Nigdzie nie ma zapisu jak sugerujesz o 18:51 i 18:52 Zaproponowałam Ci podnoszenie obu stron równania do potęgi trzeciej, (a+b)³=a³+3a²b+3ab²+b³ Eta podała Ci niemalże gotowca.

blogther: mam pytanie jak wyznacza sie dzidzine funkcji homograficznej mozecie podac jakis przykład?

blogther: oczywiscie zadnia do zrobienia

Aga1.: Zasada : mianownik różny od zera.

	4+x
np. f(x)=
	x−5

Dziedzinę zapisać można różnymi sposobami 1. D: x−5≠0⇔x≠5 2. D=R−{5} 3. D_f=(−∞, 5)U(5,∞)

blogther: okey ale ja pytam o zbior watosci no nie wiem np

	4x − 7
f(x) =		jak wyznaczyc zbor wartosci takiej funkcji
	5x +2

podałem byle jakie wspołczynniki wiec moze byc roznie

blogther: teraz zobaczyłem ze napisałem zle napisałem dzidzine a chodziło mi o zbior wartosci nie wiem jak mogłem sie tak pomylic

krystek:

	x+1		1
f(x)=		=		+2
	x−1		x−1

ZW =(−∞,2)U(2,∞)

Aga1.: Najlepiej przekształć do postaci

	a
f(x)=		+q
	x−p

Wtedy D=R−{p} ZW=R−{q} np.

	x−3		x+2−5		x+2		5		−5
f(x)=		=		=		−		=		+1
	x+2		x+2		x+2		x+2		x+2

D=R−{−2} ZW=R−{1}

Eta: Sprowadzając do postaci kanonicznej, którą podała Ci Aga1 i krystek Najprościej (bez zgaduj− zgaduli) zwyczajnie podziel

	4		33
(4x−7) : (5x+2) =		−
	5		5(5x+2)

	4
to q=
	5

	4		2
ZW= R\ {		} , D=R\ {−		}
	5		5

blogther: Eta mam pytanie jak wykonałas to dzielenie a co np w takim przypadku

	3x2 − 4
f(x) =
	x + 2

blogther: pytam jak to jest z tym wyznaczaniem ZW bo miałem takie zadanie

	x2 + 3
f(x) =
	x2 − 1

i w opowiedziach było tak to rozwiazane f(x) = k

	x2 + 3
k =		|*(x2 − 1) przy załozeniu x2 ≠1
	x2 − 1

po przedształceniach do wyznaczeni zostało cos takiego

	− 3 −k
x2 =
	1 −k

x² ≥ 0

	− 3 −k
0 ≥
	1 −k

(− 3 −k)(1 −k )≥ 0 i mam pytanie czy mozna tak robic dla kazdej funkcji czy tylko w takim przypadku jak ten?

blogther: bo jest jeszcze taki wzor na ZW funkcji homograficznej ^a_c ale jest on prawdziwy tylko dla postaci

	ax + b
f(x) =
	cx + d

Eta: Źle napisałeś zwrot nierówności: (−3−k)(1−k) ≤0 Takie zadania będziesz rozwiązywać na studiach ( badając przebieg zmienności funkcji) szkicując wykres f(x)

blogther: a w jakim dziale bo mam aktualnie teraz liczby zespolone na zajeciach

blogther: to jest cos z ekstremami lokolnymi lub globalnymi zwiazene oraz z przegieciem funkcji? tak?

blogther: dlaczego zle przeciaz x² nie moze byc ujemny?

blogther: a mam pytanie jak zrobiłas to dzielenie (4x−7) : (5x+2)?

Eta:

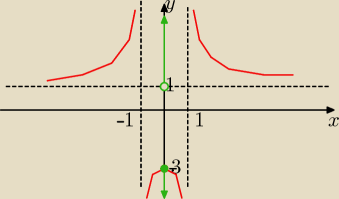
	x2−3
f(x)=		Df=R \ {−1,1}
	x2−1

y=1 asymptota pozioma x=−1 i x=1 asymptoty pionowe ZW= (−∞,−3> U (1,∞) Teraz idę zjeść ......coś dobrego

Eta:

	4
( 4x−7 ) : (5x+2)=
	5

	8
−4x −
	5

−−−−−−−−−

	−33
=		−− reszta
	5

	4x−7		4		33
to:		=		−
	5x+2		5		5(5x+2)

blogther: no i taki ZW wyszedł w opowiedzi pomimo tego ze napisałas ze zle napisałem znak nierownosci

Eta: Napisałeś tak: 0≥(−3−k)(1−k) ⇒ (−3−k)(1−k) ≤ 0 a powinieneś napisać : (−3−k)(1−k)≥0 dlatego napisałam,że źle

blogther: tak masz racje

Eta:

blogther: ale ten sposob jest poprwny wiec nie ma chyba problemu

	5x
okey to jeszcze takie pytanie jak wyznaczyc taki ZW f(x) =
	x2 − 1

Maslanek: Fajny ten wcześniejszy sposób. Zapamiętam

	5x
f(x)=
	(x−1)(x+1)

p: x=0 x→−∞: f→0 x→−1⁻: f→−∞ x→−1⁺: f→∞ x→0: f→0 x→1⁻: f→−∞ x→1⁺: f→∞ x→∞: f→0 ZW: (−∞,0)∪(0,∞). Przy czym to moja pierwsza próba tym sposobem

Maslanek: ZW: R... 0 również należy. W końcu f(0)=0

blogther: ktory sposob

blogther: w odpowiedzi jest ze ZW = R

blogther: ja jak narysowałem ta funkcje to wyszło mi ze ZW = R w przedziale x ∊( − 1;1) bo i −1 i 1 sa asymptoty pionowe

Eta: R

blogther: dodatkowo w odpowiedzi jest taka podpowiedz 1 pkt za zapisanie trojmianu ax² − 5x − a = 0

blogther: ja nie rozumiem w ogole sposobu Maslanka co on tak naprawde robi?

Eta: Liczy granice

Maslanek: Ja mam pytanie skąd to? 1 pkt za zapisanie trojmianu ax2 − 5x − a = 0

blogther: to jest zadanie z akursza od operonu i w opowiedziach jest taki schemat za co punkty daja i tak tam jest napisane

Maslanek: Ale w jaki sposób i o co chodzi w ogóle?...

blogther: a ja dalej Eta nie wiem jak zrobiłas to dzielenie jak mogła bys krok po kroku napisac ub wskazac jakis link gdzie jest cos podobnego zrobione bo nic nie rozumiem z tego np skad sie wzieło to −4x − ⁸₅ i ta reszta?

blogther: nie pisze w jaki sposob do tego doszli pisze tylko za zapisanie rownanie ax² − 5x − a = 0 jest jeszcze ze delte licza i nie mam ona pierwiastkow i z tego powodu jest ZW = R

Maslanek: Ah... W ten sposób, że f(x)=a. ax² − a = 5x ax²−5x−a=0 Δ=25+4a² >0 Jeśli chodzi o rozw. Ety to zwyczajnie ręcznym sposobem dzieli wielomiany.

Maslanek: Więc tego dalej nie rozumiem...

blogther: jak ułozyłes to rownanie ? a co do sposobu Ety to ja nie umiem dzielic wielomianow tych samych stopni nawet nie wiedziałem ze tak mozna zawesze miałem doczynienia z dzielniem zawsze albo przez x −a albo przez ax² + bx + c pierwszy raz cos takiego widze dlatego jestem taki zaskoczony i nie wiem skad sie to bierze

Eta: f(x)=a

5x
	=a ⇒ (x2−1)*a=5x ⇒ ax2−5x−a=0
x2−1

Maslanek: Ja się zastanawiam jak wyglądałoby dzielenie wielomianu niższego stopnia i czy jest w ogóle sens. Dobra już rozumiem o co chodzi z tą Δ. Δ>0, więc dla każdego a mamy dwa rozwiązania. Oprócz dla jednego, x=0, wiec i a=0... Co z tym? −−−−−− Pomyśl. Masz wszystko napisane w gruncie rzeczy.

Eta: ( x−3) : (x+1)= 1 −x−1 −−−−−−

	x−3		4
= −4 −− reszta to		= 1−
	x+1		x+1

Maslanek: Aaa... Dobra. Już mam wszystko Δ>0 ⇔ a≠0 a=0 ⇒ −5x=0 ⇒ x=0 ZW=R −−−−−−−−−−−−−−− Sposób dobry. Zapamiętam

blogther: czyli oni policzyli to w ten sam sposob ktory ja prezentowałem tam wyzej

blogther: no to dzilenie tez dobra rzecz dziekuje wam za pomoc

Maslanek: W trochę inny. Zdecydowanie inny .