 z tym zadaniem męczę sie połowę dzisiejszego dnia... i dalej go nie zrobiłam!:(
Dany jest ostrosłup prawidłowy czworokątny, którego krawędź podstawy ma długość oraz krawędź
boczna jest nachylona do podstawy pod kątem . Oblicz pole przekroju tego ostrosłupa
płaszczyzną zawierającą przekątną jego podstawy i nachyloną do płaszczyzny podstawy pod kątem
.
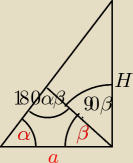
moj rysunek w skrócie jest taki (proszę mi przy okazji powiedzieć jak sie robi minus na tych
rysunkach...)
napisałam kilka zależności,lecz właasciwe nic mi z nich nie wyszło,jednak uwazam ze własnie
trzeba kombinowac na podstawie tego rysunku
z tym zadaniem męczę sie połowę dzisiejszego dnia... i dalej go nie zrobiłam!:(
Dany jest ostrosłup prawidłowy czworokątny, którego krawędź podstawy ma długość oraz krawędź
boczna jest nachylona do podstawy pod kątem . Oblicz pole przekroju tego ostrosłupa
płaszczyzną zawierającą przekątną jego podstawy i nachyloną do płaszczyzny podstawy pod kątem
.
moj rysunek w skrócie jest taki (proszę mi przy okazji powiedzieć jak sie robi minus na tych
rysunkach...)
napisałam kilka zależności,lecz właasciwe nic mi z nich nie wyszło,jednak uwazam ze własnie
trzeba kombinowac na podstawie tego rysunku
| 1 | ||
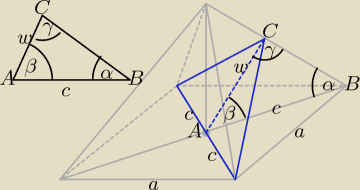
Pole powierzchni podanego przekroju P = | *2c*w = c*w | |
| 2 |
| 1 | ||
c = | a√2 | |
| 2 |
| w | c | |||
W trójkącie ABC korzystając z twierdzenia sinusów otrzymujemy: | = | . | ||
| sinα | sinγ |
| sinα | ||
Stąd w = c * | ||
| sinγ |
| 1 | sinα | |||
w = | a√2 * | |||
| 2 | sin(α + β) |

