Części wspólne zbiorów pawe: jak udowodnić, że p(A∩B)+p(A'∩B')=1 na rysunki najlepiej

pawe: ktoś?

pawe: P(A'UB')+p(A∩B)=1 gdzie A∩B to jest P(a)+P(b)−1 udowodni ktoś?

pawe: pomieszałem coś w zadaniu, wyżej jest niby dobrze

pawe: ktoś udowodni?

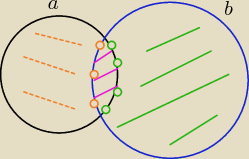
Maslanek: No więc tak: Zaznaczone na pomarańczowo: dopełnienie B (czyli B') Zaznaczone na zielono: dopełnienie A (czyli A') Oraz Różowe to część wspólna zbiorów A i B (A∩B) Jak łatwo zauważyć sumie dopełnień do A∪B brakuje A∩B − które dodajemy.

Maslanek: Co dalej. Pierwsza równość, którą podałeś jest nieprawdziwa A'∩B' ∊ ∅ Zatem: p(A∩B)+p(A'∩B')=p(A∩B)