Dziwne Kssia: W stozek o promieniu podstawy 6 i wysokosci 8 wpisano graniastoslup szesciokatny. Jedna podstawa zawiera sie w podstawie stozka, a pozostale wierzcholki naleza do powierzchni bocznej tego stozka. Oblicz objetosc graniastoslupa a najwiekszym polu powierzchni bocznej.

Eta: Pomagam Cierpliwości , narysuję rysunek! to troszke potrwa

Eta:

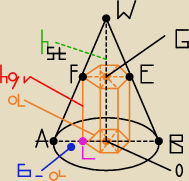
Eta: Może mało przejrzysty rys, więc dokładnie opiszę: IAOI = r = 6 IWOI= 8 ILFI= h graniast. IFGI = ILOI = a −− krawędż podst. graniast. więc : IALI = 6 −a i IWGI = 8 − h ΔAOW ~ ΔFGW więc: ^IAOI_IWOI = ^IFGI_IWGI więc ⁶₈= ^a_{8 −h} po przekształceniu tej proporcji dostaniemy: 8a = 6(8− h) => a = ³₄(8−h) teraz zajmujemy sie polem bocznym graniastosłupa: P_b = 6a*h −−− mamy zbadać maximum pola więc badamy max funkcji pola zatem: podstawiając za "a" otrzymamy: P_b(h) = 6*³₄*(8−h)*h czyli P_b(h) = −⁹₂h² +36h wykresem jest parabola ramionami zwrócona do dołu więc P_max jest dla h= −³⁶₋₉ bo ( wiesz że x_w= =^b_2a −− z funkcji kwadratowej) zatem h= 4 to a = ³₄( 8 −4) to a= 3 więc pole boczne graniastosłupa osiąga max. dla : a= 3 h= 4 teraz już tylko podstaw do wzoru na V( graniastosłupa) V= P_p *h gdzie P_p = 6*^a2√3₄ i to wszystko Pozdrawiam

Kssia: Dzieki