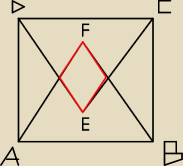
 bok kwadratu ABCDma długośc równą 2. Oblicz pole czworokąta będącego częścią
wspólną trójkątów równobocznych ABF i DEC.
bok kwadratu ABCDma długośc równą 2. Oblicz pole czworokąta będącego częścią
wspólną trójkątów równobocznych ABF i DEC.
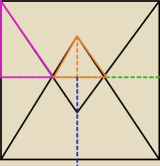 zielona linia przerywana to połowa kwadratu.
Mały pomarańczowy/brązowy trójkąt to trójkąt równoboczny o wysokości równej h=H−1, gdzie
1 to połowa boku kwadratu (na niebiesko na obrazku),
H to wysokość trójkąta równobocznego.
Trójąt rożowy/fioletowy jednak się nie przyda, ale olśniło mnie dopiero w trakcie
rysowania ;P
Jak to wszytsko wykorzystać? kombinuj ;)
Jak Ci się nie uda to napisz, ale spróbuj najpierw a nie poddawaj się po zobaczeniu
mojego obrazka ;)
zielona linia przerywana to połowa kwadratu.
Mały pomarańczowy/brązowy trójkąt to trójkąt równoboczny o wysokości równej h=H−1, gdzie
1 to połowa boku kwadratu (na niebiesko na obrazku),
H to wysokość trójkąta równobocznego.
Trójąt rożowy/fioletowy jednak się nie przyda, ale olśniło mnie dopiero w trakcie
rysowania ;P
Jak to wszytsko wykorzystać? kombinuj ;)
Jak Ci się nie uda to napisz, ale spróbuj najpierw a nie poddawaj się po zobaczeniu
mojego obrazka ;)

 a = 2
a = 2
| a√3 | ||
htrojkata duzego = | = √3
| |
| 2 |
| |FE| | 2√3 − 1 | |||
h trojkata o boku x(z mojego rysunku) = | = | |||
| 2 | 2 |
| x√3 | ||
h = | ||
| 2 |
| 2√3h | ||
x = | ||
| 3 |
| 6−√3 | ||||||||||||
x = | = | ||||||||||||
| 3 | 3 |
| 6−√3 | ||
d1 = x = | ||
| 3 |
| 6−√3 | 12√3 − 12 | |||
P = 12 * d1 * d2 = 12 * | * 2√3 − 1 = | |||
| 3 | 6 |
| 13√3 − 12 | |
| 6 |
