Oblicz wartość wyrażenia 1-tg^2x jeżeli sinx = u{2}{5} i x∊(o,u{π}{2}) micha: Oblicz wartość wyrażenia 1−tg²x jeżeli sinx = ²₅ i x∊(o,^π₂) Zupełnie nie rozumiem tego typu zadań, jest ktoś w stanie wytłumaczyć mi to w łopatologiczny sposób? Z góry dziękuję

krystek:

	sinx
tgx=
	cosx

oblicz cosx ze wzoru sin²x+cos²x=1

micha: mhm, a co oznacza to x∊(o,^π₂) ?

krystek: to znaczy ,że cosx w I ćwiartce jest dodatni.

krystek:

	4
cos2x=1−
	25

	21
cos2x=
	25

	√21		√21
cosx=		lub cosx=−		∉ do dziedziny− odpada.
	5		5

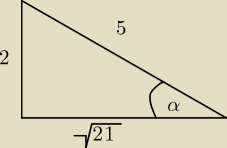
krystek: lub tak ponieważ mamy ostre kąty x∊(0,^π₂) tgx=U{2}{√21

micha: w dalszym ciągu nie rozumiem nie da się tego dokładniej rozpisać? − tak od początku do końca − przepraszam za kłopot :<

krystek:

	2		2√21
tgx=		=
	√21		21

micha: * chodzi mi o te obliczenia

krystek: Postaraj sie samodzielnie liczyć !

zią: sin²x = ⁴₂₅ sin²x + cos²x = 1 ===> cos²x = 1 − sin²x = 1 − ⁴₂₅ cos²x = ²¹₂₅ / √ cosx = ^√21₅

	25
tgx=
	√215

tgx=²₅ x ⁵_√21 tgx=²₁ x ¹_√21 tgx=²_√21

	2√21
tgx=
	21