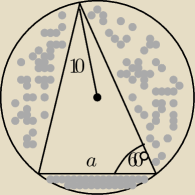
Oblicz pole zacieniowanej figury russel: Oblicz pole zacieniowanej figury (chodzi o fragment koła bez trójkąta) a = 10√2 proszę o pomoc PS Jak ładnie zacieniować figurę?

Maslanek: Zielony+niebieski = 60 Różowy − 120 (kąt środkowy oparty na tym samym łuku co wpisany) Wtedy pomarańczowy+czarny = 240 Czerwony − 30 Pomarańczowy = 180 − 2zielony 2 Czerwony + 2 zielony = czarny Ale: w trójkącie n,cz,n mamy boki 10, 10√2, 10 − zatem niebieski =45. Wtedy: P_zac = P_k − 1/2 * 10 * 10 *sin120 − 1/2 * 10 * 10 * sin 150 − 1/2*10*10 Mogłem coś poplątać

Maslanek: Fajnie.. Był rysunek

Maslanek:

pigor: ... np. tak : niech α, x − miara kąta naprzeciw boku a i długość boku naprzeciw kata 60^o odpowiednio, to z tw. sinusów

a		x		a		10√2		√2
	=2*10 i		=2*10 ⇒ sinα=		=		=		i
sinα		sin60o		20		20		2

	√3
x=20		⇒ α=45o i x=10√3 , zatem 3−ci kąt ma miarę β=75o ,
	2

więc P_Δ=¹₂axsinβ=¹₂10√2*10√3sin75^o=10√3sin75^o , gdzie np. sin75^o=sin(45^o+30^o))=sin45^ocos30^o+sin30^ocos45^o=¹₄√2(√3+1), więc P_Δ=10√3*¹₄√2{1+√3)=⁵₂√6(1+√3) , zatem szukane pole : P_z=π10²−⁵₂√6(1+√3)=⁵₂(40π−√2(3+√3))=⁵₂(40π−3√2−√6) .