 Proszę o pomoc
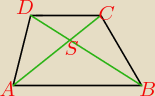
Proszę o pomoc Punkt S jest punktem przecięcia przekątnych trapezu ABCD:
a) uzasadnij, że trójkąty ABS i CDS są podobne, a trójkąty ASD i BCS mają równe pola.
b) Pole trójkąta ABS jest równe 9, a pole trójkąta CDS jest równe 4. Oblicz pole trapezu.
c)Długości podstaw trapezu wynoszą 5 i 3, a jego pole jest równe 32. Oblicz pole trójkąta ASD.
Punkt S jest punktem przecięcia przekątnych trapezu ABCD:
a) uzasadnij, że trójkąty ABS i CDS są podobne, a trójkąty ASD i BCS mają równe pola.
b) Pole trójkąta ABS jest równe 9, a pole trójkąta CDS jest równe 4. Oblicz pole trapezu.
c)Długości podstaw trapezu wynoszą 5 i 3, a jego pole jest równe 32. Oblicz pole trójkąta ASD.
 Ze względu na upał ...........mam "dzień dobroci"
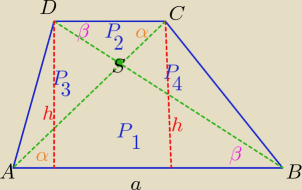
Ze względu na upał ...........mam "dzień dobroci"  a) z cechy (kkk) ΔABS ~ ΔDCS
P(ΔABC)= P(ΔABD) ⇒ P1+P3= P1+P4 ⇒ P3=P4
b)Jest taki fajny wzorek :
P(tr)= (k+1)2*P2 , k>0 −− skala podobieństwa ΔABS i CDS
a) z cechy (kkk) ΔABS ~ ΔDCS
P(ΔABC)= P(ΔABD) ⇒ P1+P3= P1+P4 ⇒ P3=P4
b)Jest taki fajny wzorek :
P(tr)= (k+1)2*P2 , k>0 −− skala podobieństwa ΔABS i CDS
| P1 | 9 | 3 | ||||
= k2 ⇒ k2= | ⇒ k= | |||||
| P2 | 4 | 2 |
| 3 | ||
P(tr)= ( | +1)2*4=................. = 25 | |
| 2 |
| a | 5 | |||
k= | = | |||
| b | 3 |
| 5 | 64 | 9 | ||||
P(tr)= ( | +1)2*P2 ⇒ | *P2= 32 ⇒ P2= | ||||
| 3 | 9 | 2 |
| 15 | ||
to: P3= k*P2= .......... = | ||
| 2 |

| P' | ||
Zatem | = k2. | |
| P |


 P(tr)= ( √P1+√P2)2 gdzie P3=P4= √P1*P2
P(tr)= ( √P1+√P2)2 gdzie P3=P4= √P1*P2
 A czemu P3=k*P2?
A czemu P3=k*P2? 

 A temu
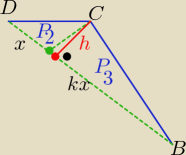
A temu  ,że
,że
| k*x*h | x*h | |||
P3= | P2= | ⇒ P3= k*P2 | ||
| 2 | 2 |
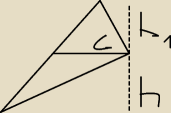 Wytłumaczysz mi czemu P = 1/2 c*h1 + 1/2 c*h2, mentorko?
Wytłumaczysz mi czemu P = 1/2 c*h1 + 1/2 c*h2, mentorko? 
 . Głęboką analizę przeprowadzam
. Głęboką analizę przeprowadzam 


 Mam nadzieję, że jabłko w ramach czekania na odpowiedź
Mam nadzieję, że jabłko w ramach czekania na odpowiedź 
