Ciekawe Godzio: Ajtek, na początek Wykaż, że stosunek długości przekątnej pięciokąta foremnego o boku "a" do długosci boku tego pięciokąta jest złotą liczbą

Mila: Ajtek, zrób to zadanie, można potem łatwo obliczyć wartości funkcji trygonometrycznych 18⁰,36⁰,72⁰.

Godzio: Odświeżam

Maslanek: Only for Ajtek? ;>

Ajtek: Cześć Godzio, wezme sie za chwile, tylko nie wiem jak szybko zrobie, bo mam troche innej roboty .

Godzio: Maslanek jak chcesz to zrób, nie widzę przeszkód, Ajtek będzie robić nie patrząc na Twoje rozwiązanie prawda ? Ja tym czasem wychodzę

Maslanek: Wyjaśnij mi równość

Ajtek: pimka, ten wątek nie dotyczy darmozjadów. Godzio czasami mi wrzuca zadanka do zrobienia, ot tak dla przyjemności .

Ajtek: O, ktoś coś usunął .

Ajtek: O! hej Mila, przepraszam nie zauważyłem Ciebie na początku .

Ajtek: Jestem, mam problem ze zrozumieniem złotej liczby, ale nad tym pracuję. Rozwiązanie zatem zapewne się przeciągnie do jutra. Dlaczego tak późno? Skorzystałem z pięknej pogody i na rower wsiadłem Pojeździłm trochę po okolicy, później miałem randkę matematyczną, przed chwilą wróciłem.

Godzio: A ja najpierw randka, a potem rower

Ajtek: Siedzę, myślę i nic konstruktywnego mi nie wychodzi .

Godzio: Myśl dalej, to nie jest trudne zadanie

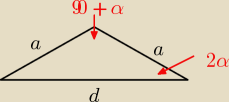
Ajtek: Dzięki za pocieszenie . Masz moje wypociny: α=x=18^o z Δ równoramiennego mamy: tw. cosinusów: d²=2a²−2a²cos(90+x) Natomiast, z pięciokąta na mocy tw. Ptolemeusza: d²=a²+ad, o ile je dobrze interpretuję. I pytanie moje brzmi co dalej? Bo obliczenia, przekształcenia do niczego mnie nie prowadzą,

	1+√5
tzn. za nic nie chce mi wyjść d=		*a
	2

Skoryguj mnie proszę, jeżeli robię gdzieś WIELBŁĄDA .

Vax: Nie patrz na twierdzenie cosinusów, tylko z samego Ptolemeusza, dobrze masz: d² − ad − a² = 0 Teraz przyjmij, że jest to trójmian kwadratowy względem niewiadomej d, liczysz deltę, wychodzi tylko jedno dodatnie rozwiązanie

Ajtek: Kurcze, lubie sobie zakombinować . Dzięki Vax . Dlaczego ja najprostsze rozwiązanie zawsze rozpatruję na końcu .

Godzio: Łojej To aż Ptolemeusza trzeba było do tego zaciągać

Godzio: Ale w takim razie gorzej dla Ciebie Mila na początku o czymś wspomniała, niestety nie zrobiłeś tego w zadaniu, poszedłeś na łatwiznę, więc część dalsza:

	√5 − 1
Pokaż, że sin18p =
	4

Godzio: sin18^o oczywiście

Ajtek: Godzio, tak wyszło. Dzięki temu przypomniałem sobie, że takowe jest . Jak masz inny sposób, to daj jakąś podpowiedź, powalczę jak włączę myślenie .

Ajtek: To coś z tw. cosinusów chyba powalczyć trzeba, ryzunek zgodny z tym co wyżej ?

Godzio: Hmmm, tam można wsadzić konkretne kąty, bo je znamy . A twierdzenie cosinusów też nie jest potrzebne

Ajtek: Z jedynki trygonomertycznej?

Godzio: Kombinuj,masz narzędzia, teraz trzeba je wykorzystać

Ajtek: Ta narzędzia. Młotek i śrubokręt pod ręką

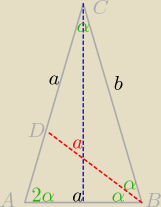
Ajtek: Δ ABC jest równoramienny i α=36^o.

	a   2		a
Z Δ ABC sin18o=		=		⇒ a=2bsin18o
	b		2b

Δ ABD jest równoramienny i podobny do Δ ABC (kkk) stąd:

a		b−a
	=		⇒ a2=b2−ab
b		a

Podstawiając a=2bsin18^o: 4b²sin²18^o=b²−2bsin18^o*b 4b²sin²18^o=b²−2b²sin18^o /:b² 4sin²18^o+2sin18^o−1=0 Δ=4+16=20 √Δ=2√5

	−2−2√5		−1−√5
sin118o=		=		odrzucamy bo mniejsze od zera,
	8		4

	−2+2√5		−1+√5{4}		√5−1
sin218o=		=		=
	8		4		4

c.n.u. Chyba wszystko zrozumiałe jest .

Ajtek: Widziałeś już to rozwiązanie

Godzio: Ok

Ajtek: uffffffffffffffffff