rozwiąż równanie
ASD: Ix
2−xI − Ix−5I ≤ 3 nie wiem jak mam rozpatrzyc pierwszy moduł

30 kwi 20:05
Maslanek: x2−x = x(x−1)
Więc dla x∊(−∞,0)∪(1,∞) i dla x∊<0,1>
Od nierówności x(x−1)≥0 i ≤0
30 kwi 20:07
Basiek: x
2−x=x(x−1) Jak ta parabolka będzie się zachowywać w odpowiednich przedziałach?

30 kwi 20:07
Maslanek: Do matury się ucz

30 kwi 20:07
krystek: ja f kwadratową x(x−1) ≥0 dla x(−∞,0) U(1,∞)
<0 dla x∊(0,1)
30 kwi 20:07
Maslanek: Tak zapytam z ciekawości. Pierwszy przypadek rozpatrujecie dla ujemnych czy dodatnich, jeśli
chodzi o takie funkcje?

30 kwi 20:09
Basiek: Maslanek− nie wiem, czy to o maturze było do mnie..., ale chwilowo trochę nie na miejscu.

I nie wiem, o co CI chodzi z tym pytaniem

30 kwi 20:11
Maslanek: Tak mi się wydawało, że maturę zdajesz?

No pytam czy tak statystycznie zaczynacie rozpatrywać przypadek f.kwadratowej w module od
ujemnych czy dodatnich. Z czystej ciekawości.

30 kwi 20:12
Basiek: Zależy. Ja zawsze małe wykresiątko i po kolei od lewej jadę

Mnie też się tak zdaje z tą maturą

A przynajmniej tak mi mówią

30 kwi 20:13
ASD: czyli x
2−x będzie dla przedziału x∊(−
∞,0)∪(1,
∞) , a −x
2+x dla x∊<0,1>

30 kwi 20:14
Maslanek: Tak.
Fajnie, że ja mam jeszcze roczek

30 kwi 20:16
Basiek: Dokładnie

30 kwi 20:16
Basiek: Powiem Ci, że ja już mam dość szkoły, stąd... z jednej strony matura, ale z drugiej "wolność"

30 kwi 20:17
Maslanek: Na razie maturka mi zwisa. I jakoś wybitnie się to pewnie nie zmieni. Jakieś tam przygotowania
będą, ale już teraz myślę, że spokojnie można by podejść. Tylko kombinatorykę ogarnąć.
Tylko, że nie można. A szkoda

30 kwi 20:18
Maslanek: A szkoła fajna. Przyjdę, pośmieję się i wyjdę

30 kwi 20:19
Basiek: Moja też tak wygląda.

A chyba nie tego oczekiwałam. Trochę mnie te 3 lata tam zmieniły,
kiedyś byłabym już obkuta i spokojnie powtarzała, na tę chwilę "mam jeszcze czas" oraz "za rok
też jest matura"

30 kwi 20:21
Maslanek: 
Przynajmniej jest wesoło

30 kwi 20:22
Basiek: To mnie właśnie przeraża.

30 kwi 20:24
30 kwi 20:37
Gustlik:
Ix
2−xI − Ix−5I ≤ 3
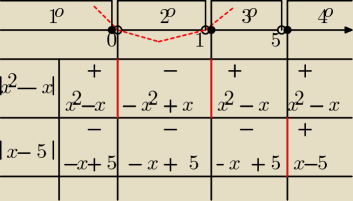
Wyznaczasz miejsca zerowe wszystkich modułów, a potem metoda "osi i tabelki":
x
2−x=x(x−1), m. zerowe to to 0 i 1, a dla modułu |x−5| m. zerowym jest 5.
Odczytujesz kolumnami:
1
o x
2−x−(−x+5)≤3 i x∊(−
∞, 0>
2
o −x
2+x−(−x+5)≤3 i x
∞(0, 1)
3
o x
2−x−(−x+5)≤3 i x∊<1, 5) zkorzystaj z 1
o, bo masz tę samą nierówność
4
o x
2−x−(x−5)≤3 i x∊<5, +
∞)
W każdym z tych 4 przypadków wynikiem będzie część wspólna rozwiązania nierówności i założenia,
a wynikiem końcowym suma 1
oU2
oU3
oU4
o.
Spróbuj rozwiązać.
1 maj 00:29




 I nie wiem, o co CI chodzi z tym pytaniem
I nie wiem, o co CI chodzi z tym pytaniem 
 No pytam czy tak statystycznie zaczynacie rozpatrywać przypadek f.kwadratowej w module od
ujemnych czy dodatnich. Z czystej ciekawości.
No pytam czy tak statystycznie zaczynacie rozpatrywać przypadek f.kwadratowej w module od
ujemnych czy dodatnich. Z czystej ciekawości. 
 Mnie też się tak zdaje z tą maturą
Mnie też się tak zdaje z tą maturą A przynajmniej tak mi mówią
A przynajmniej tak mi mówią






 A chyba nie tego oczekiwałam. Trochę mnie te 3 lata tam zmieniły,
kiedyś byłabym już obkuta i spokojnie powtarzała, na tę chwilę "mam jeszcze czas" oraz "za rok
też jest matura"
A chyba nie tego oczekiwałam. Trochę mnie te 3 lata tam zmieniły,
kiedyś byłabym już obkuta i spokojnie powtarzała, na tę chwilę "mam jeszcze czas" oraz "za rok
też jest matura" 
 Przynajmniej jest wesoło
Przynajmniej jest wesoło 



 Tak apropo to za 3 dni mi się zaczyna
Tak apropo to za 3 dni mi się zaczyna 
 Ix2−xI − Ix−5I ≤ 3
Wyznaczasz miejsca zerowe wszystkich modułów, a potem metoda "osi i tabelki":
x2−x=x(x−1), m. zerowe to to 0 i 1, a dla modułu |x−5| m. zerowym jest 5.
Odczytujesz kolumnami:
1o x2−x−(−x+5)≤3 i x∊(−∞, 0>
2o −x2+x−(−x+5)≤3 i x∞(0, 1)
3o x2−x−(−x+5)≤3 i x∊<1, 5) zkorzystaj z 1o, bo masz tę samą nierówność
4o x2−x−(x−5)≤3 i x∊<5, +∞)
W każdym z tych 4 przypadków wynikiem będzie część wspólna rozwiązania nierówności i założenia,
a wynikiem końcowym suma 1oU2oU3oU4o.
Spróbuj rozwiązać.
Ix2−xI − Ix−5I ≤ 3
Wyznaczasz miejsca zerowe wszystkich modułów, a potem metoda "osi i tabelki":
x2−x=x(x−1), m. zerowe to to 0 i 1, a dla modułu |x−5| m. zerowym jest 5.
Odczytujesz kolumnami:
1o x2−x−(−x+5)≤3 i x∊(−∞, 0>
2o −x2+x−(−x+5)≤3 i x∞(0, 1)
3o x2−x−(−x+5)≤3 i x∊<1, 5) zkorzystaj z 1o, bo masz tę samą nierówność
4o x2−x−(x−5)≤3 i x∊<5, +∞)
W każdym z tych 4 przypadków wynikiem będzie część wspólna rozwiązania nierówności i założenia,
a wynikiem końcowym suma 1oU2oU3oU4o.
Spróbuj rozwiązać.