okrąg o środku w punkcie (4,-2) jest styczny do osi OX. Okrąg ten przekształcono HELP!!!: ,Bardzo proszę o pomoc okrąg o środku w punkcie (4,−2) jest styczny do osi OX. Okrąg ten przekształcono przez jednokładność w skali k= −3/2 i środku w punkcie P należącym do prostej x+2y=0. W ten sposób otrzymano okrąg O₂. Podaj równanie okręgu O₂ jeśli a) jest on styczny do osi OX b) jest on styczny do osi OY

HELP!!!: naprawdę nikt nie może mi pomóc...

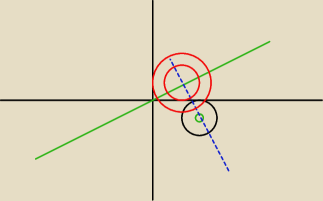
Skipper: − napisz równanie prostej przez punkt (4, −2) i prostopadłej do x+2y=0 − wyznacz punkt przecięcia będzie on środkiem jednokładności − znając go i skalę jednokładności wyznacz środek okręgu po przekształceniu ... dalej to już chyba jasne ...−

Mila: Narysuj okrąg w układzie wsp. oraz prostą x+2y=0 Środek okręgu A=(4,−2) należy do prostej x+2y=0 r=2 wynika to ze styczności do osi OX

	3
R=2*|−		|
	2

R=3 Środek okręgu jednokładnego i stycznego do osi OX i Oy też leży na prostej x+2y=0. rysujemy prostą y=3 punkt przecięcia z prostą y=−0,5x będzie jednym z okręgów S₁=(−6,3) równanie okręgu: (x+6)²+(y−3)²=9 dokończ

Skipper: ...no tak prosta nie w tą stronę−:(

Mila: Zdarza się, Skipper. Musimy się poprawiać wzajemnie. Dlatego to forum jest dobre.

HELP!!!: dziękuję Wam bardzo ale mam jeszcze jedno pytanie dlaczego mam narysować prostą y=3? Może nie jasno to ujęłam, ale to zadanie ma dwa podpunkty − I przypadek to gdy okrąg jest styczny do osi OX, warunki te się nie łączą...

Mila: Okrąg ma mieć promień 3, zatem odległość środka od osi Ox ma wynosić 3, zatem jedna prosta to y=3, druga y=−3 ( otrzymasz następny środek okręgu) to samo z okręgami stycznymi do drugiej osi, tu będą proste x=3 i x=−3. Czy to rozważyłaś? Cięzko jest mi to narysować, może Skipper to zrobiłby, poproś, ładnie rysuje.