funkcja kwadratowa ...: Wytłumaczy ktoś? Naszkicuj wykres funkcji f(x)=|x²−5x+3|. Korzystając z wykresu funkcji f, podaj rozwiązania równania |x²−5x+3|=3 O co chodzi z tym odczytaniem rozwiązań równania, bo jak z tak zrytego wykresu to odczytać? Mógłby ktoś to narysować i powiedzieć o co chodzi?

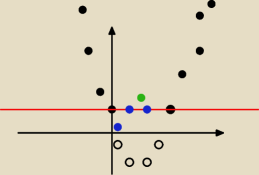
Maslanek: Zasadniczo to nie umiem rysować Ale powiedzmy, że coś takiego f(0)=3 f(1)=1 f(2)=3 f(3)=3 f(4)=1 f(5)=3 f(6)=9 No i to koniec. Więc punkty przecięcia f(x) z prostą y=3 to x∊{0, 2, 3, 5}

Saizou : najpierw narysuj funkcję f(x)=x²−5x+3, następnie nałóż moduł wartości bezwzględnej, a poźniej odczytaj dla jakich argumentów funkcja przyjmuje wartość 3

...: dzięki już wiem o co chodzi

...: Mam jeszcze jedno pytanko Znajdź te wartości parametru m, dla których funkcja f(x)=x²+mx+9 ma dwa miejsca zerowe większe od 2. 1^o Δ>0 2^o f(2) >0 3^o p >2 Pierwsze i trzecie założenie jest bardzo oczywiste, ale dlaczego musi być te drugie?

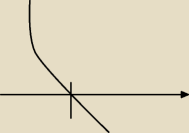
Maslanek: Bo wierzchołek musi być poza 2. Oraz wartości po 2 muszą być mniejsze od 0 (nie miejsca zerowe, ale po miejscach). Gdyby f(2)<0 oznaczałoby to, że miejsce zerowe zostało już przekroczone.

...: ok chyba łapię dzięki

...: dobry f. kwadratowa cd. Dla jakich wartości parametru k równanie (k+1)x²+2x+1=0 ma dwa rozwiązania przeciwnych znaków? zal.: k≠−1 Δ>0 x₁*x₂<0 Z tego ostatniego założenia wychodzi mi 1<0 co jest sprzecznością, a z delty k<0 to rozwiązaniem będzie k∊(−∞,0)/{−1} czy zbiór pusty, a może źle zrobiłem?

Ajtek: W trzecim założeniu zgubiłeś k.

	c
x1*x2=
	a

c=1 a=k+1

...: ¹_k+1<0 czyli k∊(−∞,−1) i to będzie całym rozwiązaniem jak mniemam ?

Ajtek: Na to wychodzi .

...: Wyznacz te wartości parametru m, dla których równanie x²+mx+9=0 ma dwa rozwiązania mniejsze od −1. zal.: {Δ>0 => m∊(−∞,−6)∪(6,∞) {f(−1)<0 => m>10 {p<−1 => m>1 Wyszło mi że m∊ (10, +∞) a powinno wyjść (6,10). Co jest źle i dlaczego

...: poszukuję chętnych

Mateusz: nic nie wychodzi

kiki93: a można to pierwsze zadanie jakoś z odbicie symetrycznego zwgl osi OX bo przecież ten fx jest w module......

Michasia: nie

kiki93: why not

...: to powie mi ktoś co tu jest źle?

f: f(x) = x²+mx+9 x²+mx+9 = 0 Δ=m²−36=(m−6)(m+6) Δ>0 m ∊ (−∞,−6)u(6,∞) f(−1) > 0 (nad −1 wykres już ma być powyżej osi x) // tu był błąd 10 − m > 0 m < 10 i jeszcze np. wierzchołek paraboli mniejszy od −1 −^m₂ < −1 ^m₂ > 1 m > 2 m ∊ (6,10)

paulinka93: można to pierwsze zadanie jakoś z odbicie symetrycznego zwgl osi OX bo przecież ten fx jest w module......

...: ok dzięki Funkcja liniowa f określona jest w następujący sposób: {^2x2+7x+6_x+2 dla x≠−2 => y=x−³₂ f(x)={ {c dla x=−2 Żeby obliczyć c powinienem chyba podstawić w y x=−2 i to wychodzi ⁻⁷₂ bodajże, a w odp. jest c=−1...

...: odświeżamy

paulinka93: może ktoś odpowiedziec na moje pytanie?: (

Mila: Paulinko można.

f: 2x²+7x+6 = 0 Δ = 49 − 48 = 1 2(x+2)(x+3/2) = 0 y = 2x+3

paulinka93: Mila dziękuję

...: eh no tak nie pomyślałem jeszcze raz dzięki

...: pytań ciąg dalszy Dla jakich wartości parametru a równanie 2a²−(a+2)x+1=0 ma dwa pierwiastki, których suma jest liczbą z przedziału <−1;1>? nie bardzo wiem co począć z tym przedziałem. Jakie dodatkowe zal do Δ>0 i a≠0?

...: up

...: pomoże ktoś?

Maslanek: Nie powinno być 2ax²? Wtedy: a≠0 Δ>0 (niech będą różne). x₁+x₂≥−1 x₂+x₂≤1

...: tak, tak jak zwykle czegoś nie przepisałem... dzięki

...: Dla jakich wartości parametru m równanie x²+3x− ^m−2_m−3 =0 ma pierwiastki rzeczywiste? moje założenia to m≠3 i Δ≥0. dochodzę do {13m−35}{m−3}>0. Jak to się rozpisywało? 13m−35>0 i m−3>0?

...: w górę idziesz

DżejDżej: żeby to równanie miało pierwiastki rzeczywiste to m≠3 Δ<0

DżejDżej:

	m−2
x2+3x+		=0
	m−3

	4m−4		9m−27+4m−4		13m−31
Δ9+		=		=
	m−3		m−3		m−3

13m−31
	<0
m−3

(13m−31)(m−3)<0 robisz rysunek

	13
m∊(		, 3)
	31

DżejDżej: chyba się nigdzie w obliczeniach nie pomyliłem...

...: odp jest (−∞,³⁵₁₃∪(3,∞). Mógłbyś mi powiedzieć dlaczego Δ<0 przecież wtedy równanie nie ma żadnych pierwiastków?

DżejDżej: heh... nie doczytałem, moja pomyłka Δ>0

...: Δ=9+^4m−8_m−3=^13m−35_m−3

...: ale dalej nie kminie dlaczego pierwszy przedział jest domknięty?

DżejDżej: pierwiastki rzeczywiste czyli może miec 2 różne pierwiastki Δ>0 a(x−x₁)(x−x₂)=0 lub tzw pierwiastek kwadratowy dlaΔ≥0 a(x−x₀)=0

	35
wniosek Δ≥0 dla tego domknięty z od strony		, a otwarty dla 3 bo ją z dziedziny
	13

wyrzuciłeś

...: aha no tak pierwiastek kwadratowy racja. Ja kierowałem się tym, że dla Δ=0 jest tylko jeden pierwiastek dlatego odrzuciłem Δ≥0, a nie pomyślałem o jego "kwadratowości"... Dzięki

...: Dana jest funkcja f(x)=x²−3. Znajdź miejsca zerowe funkcji g(x)=[f(x)], gdzie [a] oznacza największą liczbę całkowitą nie większą niż a. Mógłby mi to ktoś wytłumaczyć tak bardziej na chłopski rozum?

...: up

...: poszukuję chętnych

Maslanek: Skasowało mi się... [0,1]=0 [1]=0 [−0,5]=−1 [1,2] = 1 [2,99999] = 2 itd. g(x) = [f(x)] g(x) = 0 ⇔ [f(x)] = 0 ⇔ f(x)≥0 oraz f(x)<1. Rozwiąż takie nierówności.

...: szczerze się przyznam ze dalej tego nie ogarniam o co chodzi z tym nawiasem kwadratowym?

...: odświeżam wczorajsze nurtujące mnie pytanie

...: up

...: rozjaśni ktoś bardziej?

...: patrzę, że nikt się nie podejmuje... no trudno

...: Mam problem z zadankiem... Pomożecie? Funkcja kwadratowa g ma dwa miejsca zerowe. Ich iloczyn jest równy 2, a suma ich sześcianów równa jest 95. Znajdź równanie prostej, która jest osią symetrii wykresu funkcji g. Rozpisałem te wzory Viete'a, wyznzczylem z nich a i zapisałem funkcję jako y=ax²+bx+c. C z tym dalej robić?

...: odświeżamy

...: no może teraz się uda

ZKS: x₁x₂ = 2 x₁³ + x₂³ = (x₁ + x₂)(x₁² − x₁x₂ + x₂²) = (x₁ + x₂)[(x₁ + x₂)² − 3x₁x₂)] (x₁ + x₂)[(x₁ + x₂)² − 3x₁x₂)] = 95

	b		b2
−		* (		− 6) = 95
	a		a2

	b3		b
−		+ 6		− 95 = 0
	a3		a

b
	= t
a

t³ − 6t + 95 = 0 t³ + 125 − 6t − 30 = 0 (t + 5)(t² − 5t + 25) − 6(t + 5) = 0 (t + 5)(t² − 5t + 19) = 0

b
	= −5 / : (−2)
a

	b		5
−		=
	2a		2

	5
Więc prosta która jest osią symetrii ma równanie x =
	2

...: Dzięki wielkie ZKS

ZKS: Proszę.

...: ZADANIE Dla jakich wartości parametru m funkcja {(m−1)x +m dla x<1 f(x)={ {x² + (m−2)x+4 − 2m dla x≥1 przyjmuje tylko dodatnie wartości? Prosiłbym o dokładne wytłumaczenie dlaczego takie, a nie inne założenia są potrzebne.

justyna: zbiorem wartości funkcji kwadratowej g jest przedział (−∞, 5>, a zbiorem rozwiązań nierówności g(x)>0 jest przedział (2,8). wyznacz wzór funkcji g.

justyna: rozwiąż równanie (2x +1) + (2x + 4) + (2x + 7) +...+ (2x + 28) = 155, jeśli wiadomo, że składniki po lewej stronie są kolejnymi wyrazami pewnego ciągu arytmetycznego. Kompletnie nie wiem, jak się to zabrać...

...: wytłumaczy ktoś te moje zadanko?

...: poszukuje chętnych