Zbiór wartośći funkcji? PJ :): Mam problem z wyznaczeniem ZBIORU WARTOŚCI funkcji:

	1
f(x)=
	x2−4x+3

	1
f(x)=
	x2+x+4

Proszę o pomoc

Maslanek: 1)

	1
f(x) =
	(x−3)(x−1)

Najmniejsza wartość mianownika dla 2x−4=0 => x=2. Wtedy mianownik przyjmuje wartość: −1 Zatem ZW = <−1, ∞). Bo mianownik przy miejscach zerowych (które są poza dziedziną) jest równy prawie 0. 2) mianownik Δ<0, więc jego wartość >0 ZW=(0, ∞). Bo kiedy mianownik →∞ to ułamek →0. Analogicznie, gdy jest przeciwnie.

PJ :): A jak w pierwszym, to zrobić? Mógłbyś rozpisać czym się kierować? Wierzchołkiem paraboli czy czym? W drugim czy konieczna jest znajomość pojęcia granicy ciągu itd? Bo tego jeszcze nie mieliśmy.

Maslanek: Wystarczy zdrowy rozum. Tak. Ogólnie najmniejszą wartość osiągnie w przypadku funkcji rosnącej dla minimalnej wartości tej funkcji, jeśli tylko wierzchołek może być ujemny.

Maslanek: Albo raczej, kiedy y_w<0

PJ :): A czy przy tym licznik ułamka ma jakieś znaczenie? Czy tam jest "1", "−1", "2" itd? I czy mógłbym prosić o jeszcze jaśniejsze, o ile to możliwe wytłumaczenie tego przykładu nr 2? Dlaczego to jest od zera a nie od wierzchołka?

Maslanek: y_w>0, więc ta funkcja przyjmie wartość dodatnią. Natomiast jeśli x→∞, to cały ułamek będzie niemal zerowy. Sam licznik ma znaczenie. Jeśli to będzie −1, to zazwyczaj to będą liczby ujemne w tych przypadkach. Jeśli 2, to będzie również miało znaczenie, ale kiedy y_w<0 i a>0. Na zdrowy rozum trzeba pokombinować trochę.

PJ :): PS Jak patrzę na wykres tej drugiej funkcji to jej zbiór wartości może i będzie od zera, ale chyba nie do nieskończoności...?

PJ :): Dziękuję za pomoc. A jeszcze takie coś? sin²x−5sinx+4? Za sinusa podkładamy t i też liczymy współrzędną y_w i od tej y_w w górę to będzie zbiór wartości?

Maslanek: Faktycznie, nie do nieskończoności. Przecież najmniejszą wartość jaką przyjmie to y_w=g(−1/2)=3 3/4. Więc 1/y_w = 4/15. Dobry, świeży umysł

PJ :): f(x)=sin²x−5sinx+4

f: oj, raczej nie tak co do pierwszego: na pewno nie będzie 0 w przeciwdziedzinie (oznaczało by to, że istnieje taka liczba k, że 1/k=0) pierwiastki to 1 i 3 x → −∞ ⇒ f(x) → 0 x → 1⁻ ⇒ f(x) → ∞ x → 1⁺ ⇒ f(x) → −∞ x → 3⁻ ⇒ f(x) → −∞ x → 3⁺ ⇒ f(x) → +∞ x = 2 , f(x) = −1 ZW = (−∞,−1> ∪ (0,∞) spójrz na wykres np. w wolframie pytanie teraz, jak to ładnie wytłumaczyć bez pojęcia granicy ? w drugim przykładzie, w mianowniku nie mamy pierwiastków − więc nie będzie problemów ZW będzie przedział od 0 do odwrotności najmniejszej wiartości mianownika

Maslanek: Albo sprawdzić wartości w skrajnych wartościach sin, tj. −1, 0, 1 Wtedy dla −1: 1+5+4=10 dla 1: 1−5+4=0 dla 0: 4 Więc wtedy 1/k (gdzie k to, to wyrażenie) ∊ <1/10, ∞)

Maslanek: Mój błąd, chylę głowę

PJ :): @Maslanek: Dlaczego przy funkcji: f(x)=sin²x−5sinx+4 Mam później robić 1/k? @f: Czyli pierwszego nie da się tak łatwo zrobić bez znajomości granicy funkcji?

f: może niekoniecznie nie "nie da się", chociaż w istocie polega to na liczeniu granic potrzebne jest intuicyjne zrozumienie − musimy rozważyć przypadki nie tylko najmniejszej, największej wartości w mianowniku ale i co się dzieje z wartościami funkcji przy pierwiastkach mianownika i gdy argument jest bardzo duży / mały

PJ :): Dziękuję za pomoc

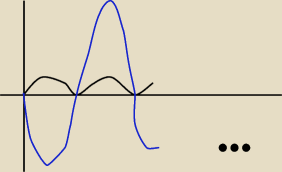
f: co do: f(x)=sin²x−5sinx+4, ładnie to możemy zrobić graficznie (szkic nie jest za bardzo w skali) jak zsumujemy pierwsze dwa składniki − wartości będą się wachać <−4,6> potem +12, to ZW = <8,18>

f: pomyłka: +4 nie +12 czyli: ZW = <0,10>

Maslanek: Skąd te +12?

Maslanek: O właśnie . Już myślałem, że jakaś czarna magia mnie spotka

f: późna godzina

Mila: f(x)=sin²x−5sinx+4 t=sinx i −1≤t≤1 i tylko w tym przedziale interesuje Cię f(t): f(t)=t²−5t+4 t_w=2,5∉<−1,1> zatem funkcja w tym przedziale jest malejąca najmniejsza wartość to f(1)=0 największa wartość to f(−1)=10 ZW_f=<0,10>

xD: hój