dowód w trójkącie lucek: Wykaż, że w trójkącie długość środkowej poprowadzonej do pewnego boku jest mniejsza od połowy sumy długości dwóch pozostałych boków tego trójkąta. Wydaję mi się, że powinno skorzystać się z nierówności w trójkącie a+b>c, ale zadanie nie chce wyjść. Prosiłbym o pomoc.

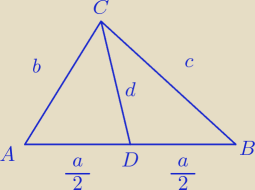
rumpek: 1^o Dla trójkąta △ADC zachodzi nierówność:

a
	+ b > d
2

2^o Dla trójkąta △BCD zachodzi nierówność:

a
	+ c > d
2

3^o Dodajemy układzik stronami:

⎧	a/2 + c > d
⎩	a/2 + b > d

a + b + c > 2d / : 2

a + b + c
	> d
2

c.n.u.

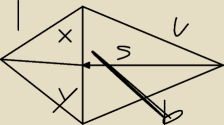
Maslanek: x+y = a b+c>2s s<1/2(b+c) Z trójkąta tworzysz równoległobok. Właśnie na to wpadłem

Maslanek: To nie ten dowód rumpek

rumpek: To co z nim nie tak specjalisto ?

Maslanek: długość środkowej poprowadzonej do pewnego boku jest mniejsza od połowy sumy długości dwóch pozostałych boków tego trójkąta. Nie na temat po prostu . Nie masz wykazać, że jest mniejszy od połowy obwodu . Też tak machnąłem, patrzę, a tu nie to co trzeba jest . Dlatego mój rysunek wygląda jak wygląda

lucek:

	a+b
Bo mam udowodnić, że d<
	2

@Maslanek Nie do końca wiem skąd ci się wzięło 2s. I skąd równoległobok skoro boki nie są równe.

rumpek: Ok, nie doczytałem "dwóch" Zwracam honor

Maslanek: Równoległobok, a nie romb. Podobnie jak przy sumowaniu wektorów po prostu jakby przesuwasz równolegle jeden z boków i zaczepiasz do drugiego. Trójkąt po lewej jest przystający do tego po prawej, więc ta środkowa jest taka sama. W związku z czym staje się przekątną równoległoboku. A oznaczenie x, y jest nieistotne. Jak mówiłem dowiodłem tego samego co rumpek, po czym deletowałem

lucek: Rozumiem już jak powstał równoległobok, ale z czego wynika, że suma dwóch boków jest większa od dłuższej przekątnej?

lucek: Przepraszam, cofam pytanie.

lucek: Dziękuję bardzo za pomoc.