Matura Godzio: Matura rozszerzona Ułożyłem powiedzmy, lekko podkręconą maturę, oczywiscie niektóre zadania są banalne, ale przy niektórych trzeba się pomęczyć. Zachęcam do zrobienia całości Zad. 1 (5 pkt) Niech A = { (x,y) : y ≥ | |x − 2| − 1 |}, B = {(x,y): y + √4x − x² − 3 ≤ 2}. Narysować na płaszczyźnie zbiór A ∩ B i obliczyć jego pole. Zad. 2 (7 pkt) Dla jakich wartości rzeczywistego parametru p równanie (p − 1)x⁴ + (p − 2)x² + p = 0 ma dokładnie dwa różne pierwiastki. Zad. 3 (8 pkt) Podstawą ostrosłupa o wysokości h jest trójkąt prostokątny o kącie ostrym α. Wszystkie ściany boczne ostrosłupa są nachylone do podstawy pod kątem α, a pole powierzchni całkowitej jest czterokrotnie większe od pola podstawy. Obliczyć objętość ostrosłupa. (dobrze by było podać odpowiedź w najprostszej postaci) Zad. 4 (6 pkt) Jednym z pierwiastków wielomianu W(x) = ax³ + bx² + cx + d jest liczba − 1. Znaleźć pozostałe pierwiastki wiedząc, że W(1) = −2 i środkiem symetrii wykresu funkcji W(x) jest punkt

	1		5
S(		,		).
	4		2

Zad. 5 (5 pkt) Rozwiązać nierówność √log₂(x² − 1) > log₂√x² − 1 Zad. 6 (5 pkt) Do zbiornika poprowadzono trzy rury. Pierwsza rura potrzebuje do napełnienia zbiornika o 4 godziny więcej niż druga, a trzecia napełnia cały zbiornik w czasie dwa razy krótszym niż pierwsza. W jakim czasie napełnia zbiornik każda z rur, jeżeli wiadomo, że wszystkie trzy rury otwarte jednocześnie napełniają zbiornik w ciągu 2 godzin i 40 minut ? Zad. 7 (5 pkt) Z przystani A wyrusza z biegiem rzeki statek do przystani B, odległej od A o 140km. Po upływie 1 godziny wyrusza za nim łódź motorowa, dopędza statek, po czym wraca do przystani A w tym momencie, w którym statek przybija do przystani B. Znaleźć prędkość biegu rzeki, jeżeli wiadomo, że w stojącej wodzie prędkość statku wynosi 16 km/godz., a prędkość łodzi 24 km/godz. . Zad. 8 (5 pkt) W pudełku jest 400 kul w tym n czerwonych.Wybieramy losowo dwie kule. Prawdopodobieństwo

	1
wylosowania dwóch kul czerwonych jest równe		.
	760

a) Ile kul czerwonych jest w tym pudełku ? b) Obliczyć prawdopodobieństwo, że żadna z wylosowanych kul nie jest czerwona Zad. 9 (5 pkt) Udowodnić, że jeżeli liczby rzeczywiste a,b,c spełniają warunki a² + b² = (a + b − c)² oraz

	a2 + (a − c)2		a − c
b,c ≠ 0 to		=
	b2 + (b − c)2		b − c

Może zadań nie jest wiele, ale

rumpek: nierówności logarytmicznej nie ma na maturze odnośnie zadania 3 to ściany padają pod takim samym kątem jaki jest kąt ostry w trójkącie prostokątnym o wysokości h [podstawa ostrosłupa] ma się rozumieć czy może β ? Bodajże, jak pamięć mnie nie zawodzi to w podstawę można wpisać okrąg

Godzio: Polecenie jest dobrze napisane, na logarytmy nie narzekaj bo i tak jest standardowe rozwiązanie

Godzio: Widzę, że coś mi przeszkodziło w dopisaniu ... Może zadań nie jest wiele, ale jak na taki poziom będzie w sam raz

elpe: zadanie 7. o ile dobrze kojarzę jest ze zbioru zadań z fizyki Jędrzejewski Kruczek Kujawski aż poszukam

Święty: Zad. 9 a²+b²=(a+b−c)² a²=(a+b−c)²−b² a²=(a−c)(a−c+2b) b²=(a+b−c)²−a² b²=(b−c)(b−c+2a)

a2+(a−c)2		(a−c)(a−c+2b)+(a−c)2
	=		=
b2+(b−c)2		(b−c)(b−c+2a)+(b−c)2

	(a−c)(2a+2b−2c)		a−c
		=		c.n.u
	(b−c)(2a+2b−2c)		b−c

Święty: Zad. 8 a) n≥1 i n∊N₊

	400 2
|Ω|=

	n 2
|A|=

	1
P(A)=
	760

n 2		1
	=
400 2		760

... n²−n−210=0 Δ=841 √Δ=29 n=−14 n=15 n≥1 i n∊N₊ ⇒ n=15 b) 400−15=385

	400 2
|Ω|=		=79800

	385 2
|B|=		=73920

	73920
P(B)=		≈0,93
	79800

rumpek:

	88
Święty pozostawiamy zawsze w ułamku zwykłym w tym wypadku: P(B) =
	95

Godzio: Święty weź się za te trudniejsze Bo widzę, że zaczynasz od banałów

Święty: Trzeba się czymś dowartościować

rumpek: Zad 3 the best of

Święty: Zad. 5 √log₂(x²−1) > log₂√x²−1 D: log₂(x²−1) ≥ 0 x∊(−∞, − √2>U<√2, ∞) x²−1>0 x∊(−∞,−1)U(1,∞) D=(−∞, − √2>U<√2, ∞)

	1
[log2(x2−1)]0,5 >		log2(x2−1)
	2

t=log₂(x²−1) <Pewnie przydałyby się tu jakieś założenia >

	1
t0,5 >		t /2
	2

	1
t >		t2
	4

t∊(0,4) log₂(x²−1)>0 x∊(−∞, − √2)U(√2, ∞) log₂(x²−1)<4 x∊( − √17,√17) Odp. x∊(−√17, −√2)U(√2,√17)

pawel nowy: jestem nowy, jak coś źle to poprawcie zadanie 2 x²=t t>0 (p−1)t²+(p−2)t+p=0 Δ>0 Δ=(p−2)²−4*p*(p−1)>0 p²−4p+4−4p²−4p>0 −3p²−8p+4>0 3p²+8p−4<0 i tutaj nie jestem pewien, bo wolfram alpha mi pokazuje że źle rozpisałem deltę

rumpek: t = x², t ≥ 0 Δ = (p − 2)² − 4p(p − 1) = p² − 4p + 4 − 4p² + 4p = −3p² + 4 > 0 dokończ sam

pawel nowy: o dzięki rumpek, pomieszałem znaki

kylo1303: Mam nadzieje ze sam tych zadan nie wymyslales, bo bedzie za trudno Zabiore sie za nie jak troche sie zrelaksuje.

crap: Godzio poprosze o podstawe ^^

Godzio: Podstawa niestety zajęłaby za dużo czasu który mi się już kończy niestety, gdybyś dał znać wczoraj to jeszcze bym coś nastrugał a tak ...

k: w zad 2 p ∊ (0, ^2√3₃) ?

k: mała pomyłka p ∊ (0,1) ?

Święty: 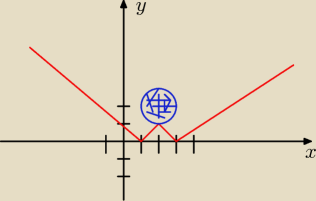A∩B 4x−x²−3≥0 x∊<1,3> y+√4x−x²−3≤2 y−2 ≤ − √4x−x²−3 /² x²+y²−4x−4y+7≤0 S=(2,2) r=1 P=πr²=1π

Godzio: Obawiam się, że nie.

Godzio: Oba rozwiązania złe

Święty:

Godzio: k. podaj warunki jakie dałeś (jak dałeś tylko jeden przypadek to pomyśl nad innymi) Święty pomyśl na tym kołem (?)

Godzio: Za 8 i 5 masz maxa (oczywiście pamiętaj, że w prawdopodobieństwie na maturze trzeba wszystko opisywać) Za zad. 1 max 2 pkt

Godzio: Koło 23 − 24 wejdę i sprawdzę rozwiązania o ile będą jakieś

ZKS: Zadania do rozwiązania maturzyści!

def: Czy w 4 wielomian W(x)=(x+1)(8x²−14x+5) ? Pozostałe pierwiastki 1/2 lub 5/4 ?

Godzio: Zgadza się

Pepsi2092: Siemano Godzio Czy w nierówności logarytmicznej odp to x∊(−√5;−√2)U(√2;√5) ?

hm: Zad6

	16
2h40min=
	6

1		1		2		6
	+		+		=		?
x		x+4		x+4		16

Godzio: Niestety nie, Święty podał poprawne rozwiązanie

Godzio: hm

Basiek: Zostało jeszcze coś do rozwiązania? Bo od poniedziałku (który już trwa) robię arkusze

Pepsi2092: Mamy nadzieje, że CKE nie inspirowała się Twoimi arkuszami próbnymi które nam dajesz

Godzio: 5,8 i 9 ma tylko pełne rozwiązania

hm: O jak dobrze, właśnie pół h temu zacząłem ogarniać tego typu zadania. Jeszcze nad tym popracuję. Rury mogą trafić się jedynie na podstawie?

Godzio: W formie podkręconej mogą pójść na rozszerzenie

hm: Oby nie

rumpek: Maturę mają ułożoną już w listopadzie

Basiek: Co do zad. drugiego, wymyśliłam takie warunki, aczkolwiek nie wiem, czy to w ogóle ma jakiś sens. Zerkniesz? więc tak: x²=t Rozpatruję 3 przypadki: 1) Δ=0 i t>0 2) Δ>0 i t₁*t₂<0 3) dla p=1 (x=−1 lub x=1)

hm: No to już napisz jakie bd te zadania xD

rumpek: Jak nikt do jutra się nie połasi na zadanie 3, to ostatecznie będę mógł zrobić

hm:

	1		5
Jak będzie w Zad 4 z tym środkiem symetrii? Jedno to że W(		)=		? Coś jeszcze do
	4		2

tego?

Basiek: Moje rozwiązanie do zad. 2:

	−2√3
dla p∊(0,1> ∪ {		}
	3

^^ Nie wygląda to wiarygodnie.

Godzio: Wyniku Ci nie powiem, bo akurat tego zadania jeszcze nie robiłem, 2 i 3 masz ok, nie wiem jak rozwiązałaś 1 przypadek

kylo1303: Zadanie 7: Odpowiedz: Predkosc rzeki wynosi 4km/h. Nie chce mi sie pisac calego rozwiazania bo raz ze jestem zmeczony a dwa ze troche namazalem na swojej kartce, ale napisze poszczegolne "wydarzenia": czas calkowity: 7h czas spotkania 3,5h droga do spotkania: 70km.

kylo1303: Zadanie 6: I kran w 12h, drugi w 8h a trzeci w 6h

kylo1303: Zadanie 4:

	1		5		5		1
W(x)=8(x−		)(x+1)(x−		) czyli pozostale pierwiastki to x1=		i x2=
	2		4		4		2

kylo1303: Zadanie 8: a) 15

	88
b)
	95

(ale to juz bylo podane na forum)

Godzio: Wszystko się zgadza

Godzio: Jeśli coś się pojawi to sprawdzę z rana, bo jak jeszcze posiedzę to coś czuje, że nie wstanę rano, niestety nie mam tyle wolnego co wy Dobranoc

kylo1303: Teraz sprobuje czegos z pierwszej trojki

kylo1303: Dobranoc Obys sie wyspal

kylo1303: Zadanie 1: (nie wiem czy sie nie walnalem gdzies)

	π
P=7−
	2

kylo1303: I tak na marginesie w twoim arkuszu jest 51pkt do zdobycia

kylo1303: Zastanawiam sie czy robienie zadan o tej porze ma sens... w kazdym badz razie w zadaniu 2 wyszlo mi:

	2√3
p∊(0,1> u {		}
	3

hm: Basiek czy w Twoim drugim warunku do zadania 2 powinna być jeszcze p−1≠0?

Godzio: kylo w pierwszym wynik zły

emagnuski: Mnie w pierwszym wyszło cosik takiego, ja czy kolega wcześniej zrobił błąd w obliczeniach?

emagnuski:

	1
P=		(π−2)
	4

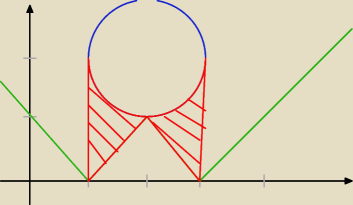
emagnuski: Hmmm, a czy to nie będzie takie coś? Na czerwono poszukiwane pole

kylo1303: No mi w tym pierwszym to oczywiscie ze wynik zly wyszedl bo nie wzialem pod uwage dziedziny xD Zaraz poprawie

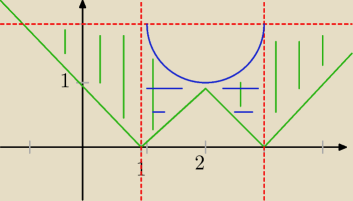
kylo1303: Cos takieg wyszlo, przy czym przerywane linie to ograniczenia z dziedziny, ale wliczaja sie do rozwiazania. Czyli na dobra sprawe wyszlo to samo co u kolegi wyzej.

	π		π
P=4−1−		=3−
	2		2

Godzio: Teraz jest ok emagnuski o to pole chodziło

hm: Odpowiedzcie na moje pytanie tuż zaraz wyżej

Godzio: Jakie funkcje mają środek symetrii ? Jakiej są postaci ? Nałóż te warunki, + to co masz dane i masz wzór wielomianu

kylo1303: Godzio A to zadanie 2 mam dobrze? Bo w tym pierwszym pominalem fakt ze x∊<1,3> ale jak widze juz jest okej. Liczylem ze ktos (rumpek) zrobi zadanie 3, ale widze ze nie bylo chetnych. Moze sam sprobuje, chociaz stereometrii nie lubie i szybko sie przy niej nudze.

Godzio: Sposobu rozwiązania nie ocenię, ale wynik jest ok

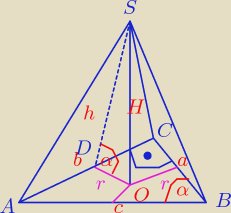
rumpek: Skoro wszystkie ściany boczne nachylone są do płaszczyzny podstawy pod kątem α, zatem wszystkie ściany boczne ostrosłupa: △ACS i △ABS i △BCS mają równą wysokość [oznaczyłem h] oraz spodek wysokości to środek okręgu wpisanego w podstawę [trójkąt prostokątny]. Suma wszystkich pól:

	1		1		1		1
1o Pc =		* a * h +		* b * h +		* c * h +		* a * b
	2		2		2		2

4P_p = 4P_c

	1		1
4 *		* ab =		* (a * h + b * h + c * h + * a * b )
	2		2

	1
2 * ab =		(a * h + b * h + c * h + * a * b) / * 2
	2

4ab = ah + bh + ch + ab 3ab = h(a + b + c)

	3ab
h =
	a + b + c

2^o Odnośnie podstawy mamy podane h_p i α.

	1		1
Pp =		a * b =		* c *hp
	2		2

ab = ch_p

	b		b
sinα =		⇒ b = sinαc ⇒ c =
	c		sinα

	a		bcosα		asinα
cosα =		⇒ cosαc = a ⇒		= a ⇒ bcosα = asinα ⇒ b =
	c		sinα		cosα

	b		asinα   cosα		a
Obliczmy jeszcze c: c =		⇒ c =		=
	sinα		sinα		cosα

	a		asinα
Mamy teraz wszystkie boki uzależnione do jednej wartości:		,		, a.
	cosα		cosα

	asinα		a
Podstawiamy pod pole ab = chp ⇒ a *		=		* hp ⇒
	cosα		cosα

a2sinα		ahp		hp
	=		⇒ a2sinα = ahp ⇒ hp = asinα ⇒ a =
cosα		cosα		sinα

No i teraz mamy wszystko uzależnione od podanej z zadania wartości α i h_p, pozostało podstawić

	H
pod boki a,b,c i na końcu obliczyć: sinα =		. Sądzę, że gdzieś się "machnąłem" z
	h

obliczeniami Dlatego wpierw czy to Godzio w miarę ? wygląda, tak się zastanawiam nad drugim sposobem mianowicie: podobieństwo trójkątów: △ABC ~ △SDO (k,k); Jakby gdzieś byłby błąd to "pardon" ale przez ten edytor dostaje oczopląsu

bialykruk: do zadania 2 warunki podstawiamy t=x² 1⁰ Δ=0 t1>0 lub 2⁰ Δ>0 t1*tx<0 ?

Godzio: bialykruk jak z tymi warunkami 1^o rozwiążesz zadanie ? Po drugie trzeba sprawdzić przypadek funkcji liniowej, po trzecie w żadnym przypadku nie widzę założenia: a ≠ 0

Godzio: rumpek wygląda dobrze, podejmiesz się podania wyniku ? Może pokaże nieco krótszy sposób

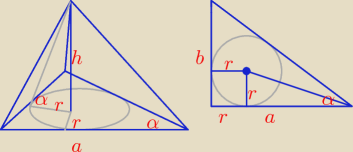
Godzio: Najpierw zacytuję twierdzenie, z którego skorzystam, a które warto znać Twierdzenie Jeśli F' jest rzutem prostokątnym figury F to S_F' = S_F * cos, gdzie α to jest kąt między płaszczyznami. Rozwiązanie: Ponieważ ściany boczne są nachylone pod tym samym kątem, to P_p = P_b * cosα co daje:

	1
cosα =		(Pb = Pc − Pp = 3Pp)
	3

	α		r		α
tg		=		⇒ a = r(1 + tg		)
	2		a − r		2

	α		α		α
a = r + r * ctg		= r(1 + ctg		) = hctgα(1 + ctg		)
	2		2		2

	α		α
b = atgα = rtgα(1 + ctg		) = h(1 + ctg		)
	2		2

	h2		α
Pp =		ctgα(1 + ctg		)2 = małe przekształcenia, dążymy do uproszczenia =
	2		2

	1 + sinα
h2ctgα *		, stąd mamy:
	1 − cosα

	1		h3		1 + sinα
V =		Pph =		ctgα		, ponieważ
	3		3		1 − cosα

	1		√8		1
cosα =		, sinα =		, ctgα =		to po elementarnych przekształceniach
	3		3		√8

mamy:

	h3
V =		(4 + 3√2)
	24

Wydaje się krótsze, bo parę męczących rzeczy pominąłem, ale wynik ładny

rumpek: Po przekształceniach powinienem otrzymać to samo

hm: Basiek chyba tęz nie napisała założenia a≠0? do pierwszych dwóch

hm: może tu tylko nie uwzględniła, bo kylo ma taki sam wynik jak ona. Dobre te wyniki?

Godzio: Zgadza się, też nie napisała

Godzio: Wyniki są ok już to pisałem

CocaCola: Przepraszam, że zmieniam temat, ale nie chcę zakładać nowego wątku. czy macie może linki do matur poprawkowych, albo pisanych w drugim terminie?

Basiek: @Hm, przecież rozpatruję a=0 (czyli p=1) w moim poście, jako przypadek trzeci. Wychodzą ładne pierwiastki x=−1 i x=1. Po co mi takie założenie? Ono jest błędne.

Basiek: Stop− czyli co? Że złe warunki? Zaczynam się naprawdę naprawdę gubić.

Godzio: Warunki są ok, ale raczej trzeba dopisać, że odrzucasz a = 0

ohayou:

	2√3
dobrze napisałaś p∊(0,1>U{		} i tyle.. a ja mam pytanie o ten wielomian bo nie
	3

rozumiem, skąd ten dodatkowy pierwiastek? ..

Basiek: @Godzio...., proszę, czytaj ze zrozumieniem. Ja napisałam, że nie odrzucam tej opcji. A Ty mówisz mi, że ... mam odrzucić, ale jest okej. nie rozumiem.

Basiek: (p − 1)x⁴ + (p − 2)x² + p = 0 gdzie t=x² (p−1)t²+(p−2)t+p=0 dla a=0, czyli p=1 −t+1=0 => 1=x² => x=1 lub x=−1 ....

ohayou: Basiek, zrobiłaś może z wielomianem?

Basiek: Nie robiłam. I nie zrobię. Zrobię dobrze− powiedzą, że źle. Zrobię źle− będzie jeszcze gorzej.

Basiek: Inna sprawa, że nie umiem.... Ale dobra, jestem zdenerwowana. Wyżywam się na innych. Przepraszam Więc... ja zrobiłabym to tak (wiem, wiem− Godzio zauważyłby jakąś parzystość, czy coś..., ale ja inaczej)− wielomian to... funkcja (chyba), mamy dwa podane punkty oraz środek symetrii. Skorzystałabym z wektorów, by wyznaczyć kolejne dwa punkty. Wtedy 4 równania− 4 niewiadome=bingo!

ohayou: a ja bym myślał o jakiś okręgach! i jak tu żyć.

Basiek: Nie, okręgów nie widzę. W ogóle, rzadko je zauważam. Wszędzie widzę wektory. Ale pogódźmy się: http://a7.sphotos.ak.fbcdn.net/hphotos-ak-ash3/560224_357045051003309_333316346709513_952072_1051495611_n.jpg

ohayou: tak, rozszerzona będzie łatwiejsza!

Basiek: Tak, czy tak... będzie źle. Obecnie myślę tylko o tym, żeby mieć to za sobą

ohayou: nie mógłby ktoś wytłumaczyć tego z wielomianem? resztę już zrobiłem...

kylo1303: Pomysł Basiek jest dobry, jak dobrze zastosujesz to wyjdzie.

Basiek:

ohayou: Basiek mogłabyś to zapisać?

Basiek: Nie. Ja jestem od pomysłów, nie od realizacji.

kamil: Basiek " Ja jestem od pomysłów, nie od realizacji " hahha ; )

Basiek: Ja zawsze jedno mówię, a robię drugie, ech... Zadanie z wielomianem A(−1,0) −> A'(a,b) B(1,−2) −> B'(c,d)

	1		5
S(		,		)
	4		2

więc : → → AS= SA'

	1		5		1		5
[		+1,		]= [ a−		,b−		]
	4		2		4		2

	3		3
a=		b=5 A'=		,5
	2		2

→ → BS= SB'

	1		5		1		5
[		−1,		+2]= [ c−		,d−		]
	4		2		4		2

	1
B'=−		,7
	2

W(x)=a(x−x₁)(x−x₂)(x−x₃) przy czym x₁=−1 W(x)=a(x+1)(x−x₂)(x−x₃) Podstawiamy punkty, wyliczamy...

Basiek: −2=2a(1−x₂)(1−x₃) 5=2,5a(1,5−x₂)(1,5−x₃) 7=1,5a(0,5−x₂)(0,5−x₃) Przy czym zaznaczam, że nigdzie nie jest napisane, że środek symetrii S należy do wykresu wielomianu Stąd.... nigdzie tego nie używam.