w blogther: W trójkącie równoramiennym ramię jest trzy razy dłuższe od podstawy. Suma długości promienia okręgu opisanego na tym trójkącie i promienia okręgu wpisanego w ten trójkąt jest równa 23. Oblicz długość ramienia tego trójkąta.

	552√35
długosc ramienia wyszła mi
	611

blogther: sprawdzi to ktos?

kylo1303: zaraz zerkne

blogther: okey

kylo1303: Wyszlo mi inaczej. Napisz jak to rozwiazywales, podaj odpowiedz jak masz. Jakie ci wyszly promienie?

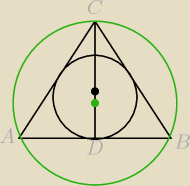
blogther: nie mam odpowiedzi nie liczyłem promienie poprostu korzystałem z wzorów P=^abc_4R=rp p = ^{3a + 3a +a} ₂

	a√35
CD =
	2

P = 0,5 * AB*CD i ty ma bład bo dałem DB wiec juz moj wynik koncowy jest zły

	a2√35
P=
	4

r = 23 − R R = ^abc_4P R = ^9a3_4P

a2√35
	= r*3a + 3a +a 2
4

	a2√35
		= (23 − R) * 7a2
	4

	a2√35
		= (23 − 9a34P) * 7a2
	4

	a2√35
		* 27a = 23 − 9a3 * a2√35
	4

blogther: musze to jeszcze raz przeliczyc chyba mam za duzo błedow a jaki tobie wyszedł wynik?

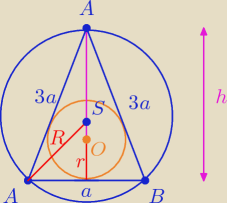
rumpek: 1^o r + R = 23

	2P		2P		2P
2o Rozpatruję promień okręgu wpisanego: r =		=		=
	a + b + c		a + 3a + 3a		7a

	1		a		a2
P =		* a * h ⇒ h2 + (		)2 = 9a2 ⇒ h2 = 9a2 −		⇒ h2 =
	2		2		4

36a2 − a2		35a2		√35a
	⇒ h2 =		⇒ h =
4		4		2

	1		√35a		a2√35
P =		* a *		=
	2		2		4

	a2√35   2		a2√35		1		a√35
r =		=		*		=
	7a		2		7a		14

	abc
3o Rozpatruję promień okręgu opisanego: R =
	4P

	9a3		9a
R =		=
	√35a2		√35

4^o Korzystam z informacji z zadania: R + r = 23

9a		a√35
	+		= 23 / * 14√35
√35		14

9a * 14 + 35a = 322√35 126a + 35a = 322√35 161a = 322√35

	322√35
a =		= 2√35 Zatem ramię ma 6√35
	161

kylo1303: x=2√35

kylo1303: Czyli ramie tak jak wyzej 3x=6√35

blogther: tak teraz sie zgadza

blogther: mam jeszcze jedno takie zadanie zaraz Ci podam link bo jest do tego zadnia wykres chodzi mi o zadanie 11 http://pliki.nowiny24.pl.s3.amazonaws.com/pdf/2012-01-16_probna_matura_matematyka_arkusz_p.rozszerzony.pdf

blogther: jak zaczasc ten podpunkt a podstawic punkt A do rownanie funkcji i wiemy jeszcze ze wykres powstał po przesunieciu funkcji o wektor 3,2

kylo1303: Zauwaz ze x≠−3 i y≠2 (asymptoty) oraz masz podany pkt A . Zapisz wzor f. wymiernej w innej postaci i podstaw to co mozesz, powinno wyjsc. Jak nie to pomoge bardziej.

blogther: okey teraz nie moge ale wroce do tego zadania za 30 min inna postac tej funkcji f(x) to ^a_x tak czy inaczej?