Zadania Godzio: Ajtek widzę, że się nudzisz Zaraz Ci coś podrzucę, ale napisz mi jeszcze, czy ze studiów mam też Ci coś dawać ?

Godzio: Na myślenie, udowodnij twierdzenie o dwusiecznej kąta, bez korzystania z twierdzenia sinusów i cosinusów

Godzio: up

ICSP: up

Tomek.Noah: z podobieństwa trojkatow albo z stosunkow pol trojkata o rownej wysokosci

Ajtek: Cześć Godzio . treaz to zauważyłem, wieczorem mnie nie było . Wiesz, wolałbym powalczyć z rozszerzeniem ze średniej. Do materiału ze studiów dojdziemy trochę później . Wezmę się za to za chwil parę, nie wiem ile mi się zejdzie, tzn. zależy od tego jak bardzo zakombinuje sobie to zadanie .

Godzio: Ok

Ajtek: Dopytam jeszcze, chodzi o tw. dwusiecznej kąta w trójkącie?

Godzio: Tak

Ajtek: Rysunek chcesz?

Godzio: No nie zaszkodzi

Ajtek: Zjem i się wezmę .

Ajtek:

|AD|		|AC|
	=
|DB|		|BC|

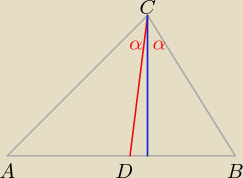
Δ−ty ADC i DBC mają taką samą wysokość. Stosunek ich pól jest równy stosunkowi długości ich podstaw.

PΔADC		|AD|
	=
PΔDBC		|DB|

	|AC|*|CD|*sinα
PΔADC=
	2

	|BC|*|CD|*sinα
PΔDBC=
	2

czyli mamy:

|AC|*|CD|*sinα   2		|AD|
	=
|BC|*|CD|*sinα   2		|DB|

Po skróceniu

|AC|		|AD|
	=
|BC|		|DB|

c.n.u. Może być? Dzięki Tomek za podpowiedź .

Godzio: Może być, ale ja chce prościej

Ajtek: Nie mam pomysłu na prościej, na tą chwilę .

Godzio: Ja też, dlatego myślę Pamiętam, że był jakiś mega szybki sposób

Ajtek: Z tw. sinusów, ale zgodnie z poleceniem nie można tego użyć .

Godzio: No nie Talesa trzeba było użyć to pamiętam na pewno i coś dorysować ...

Godzio: Później pomyślę Bo muszę wyjść na trochę, pomyśl o tym co napisałem, sposób był bardzo szybki

Vax:

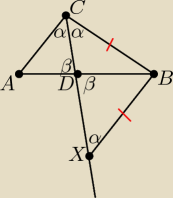
	|AD|
Na prostej CD obierzmy taki punkt X, że |BC| = |BX|, wówczas ΔADC ~ ΔXBD skąd		=
	|AC|

	|BD|		|BD|		|AD|		|AC|
		=		⇔		=		cnd.
	|BX|		|BC|		|BD|		|BC|

Godzio: Ano, chyba o to mi chodziło Dzięki Vax

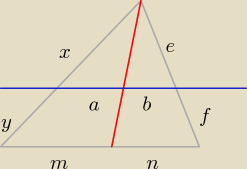
Ajtek: Takie coś wykombinowałem:

m		x+y
	=
n		e+f

x		x+y		a(x+y)
	=		⇒m=
a		m		x

e		e+f		b(e+f)
	=		⇒n=
b		n		e

m		a(x+y)   x		a(x+y)		e
	=		=		*
n		b(e+f)   e		x		b(e+f)

	a		e
I trzeba udowodnić że:		*		=1
	x		b

Ajtek: Masz jakiś pomysł?

Godzio: Ta początkowa proporcja nie zachodzi

Ajtek: Fakt

Ajtek: Dlaczego nie?, Zaczynam się gubić

Godzio: Z niczego nie wynika