planimetria hmmmm: ... i znowu mam problem: Ratownicy mający do dyspozycji linę o długości 80 metrów mają wytyczyć przy brzegu plaży kąpielisko w kształcie prostokąta (wzdłuż brzegu nie bedzie liny). Jakie wymiary powinno mieć to kąpielisko, jeżeli wczasowicze chcą, aby miało ono jak największą powierzchnię? Należy przyjąć, że brzeg plaży tworzy linię prostą. Może mi ktoś w ogóle wytłumaczyć jak rozwiązywać tego typu zadania z "największe pole", "najmniejsze z możliwych" itp... to chyba coś z pochodną powinno być, prawda? Ratujcie, bo moja matura legnie w gruzach

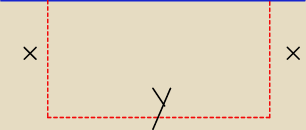
tim: czerwona to lina x + x + y = 80 2x + y = 80 y = 80 − 2x Pole = xy = x(80 − 2x) = 80x − 2x² Mamy funkcję kwadratową −2x² + 80x. Wiemy, że największą wartość ta funkcja ma w wierzchołku, gdyż a < 0, oraz Δ > 0.

	−80
xw =		= 20
	−4

Odp. Kąpielisko ma największe pole, dla x = 20, oraz y = 40 Podobne zadania 1685

Bogdan: Dzień dobry. Zaraz wyjaśnię.

hmmmm: Oki.... Dziękuje baaaaaaardzo! Już wiem o co chodzi... Życie mi ratujecie, Kocham Was normalnie... Dziękuje, dziękuje, dziękuje... Ale znając życie jeszcze się do Was zwrócę o pomoc. Pozdrawiam

Bogdan: tim już pokazał rozwiązanie. Cześć tim. Na poziomie szkoły średniej tego typu zadania, czyli zadania optymalizacyjne nie rozwiązujemy poprzez pochodną funkcji (ten materiał wypadł z programu nauczania), ale poprzez sprowadzenie do funkcji kwadratowej f(x) = ax² + bx + c, która w zależności od znaku współczynnika a ma maksimum (dla a < 0) albo ma minimum (dla a > 0). Rozwiązaniem zadania optymalizacyjnego jest odcięta wierzchołka tej paraboli, którą tim nazwał x_w. Najczęściej postępowanie jest następujące: 1. Wyznaczamy równanie z 2 niewiadomymi wynikające z treści zadania, z tego równania wyciągamy jedną z niewiadomych. 2. Zapisujemy wzór wielkości optymalizowanej, w tym wzorze występują te same dwie zmienne, które pojawiły się w równaniu, do tego wzoru wstawiamy wyciągniętą z równania zmienną. W wyniku otrzymujemy wzór paraboli, z której obliczamy współrzędną odciętą wierzchołka, ta liczba jest rozwiązaniem. Przykład. Który z prostokątów o obwodzie 100 ma największe pole powierzchni? Rozwiązanie: a, b − długości boków prostokąta. 1. 2a + 2b = 100 => b = 50 − a 2. Pole P = ab → maksimum P = a(50 − a) => P(a) = −a² + 50a

	−50
Funkcja P(a) osiąga maksimum dla a =		= 25, b = 50 − 25 = 25
	−2

Odp.: Prostokąt o największym polu powierzchni i obwodzie 100 jest kwadratem o boku 25.