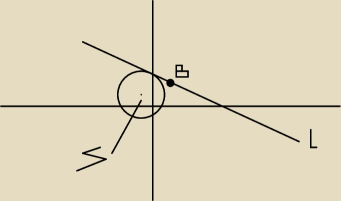
geom. analit. Efka: dany jest okrąg o równaniu: x²+y²+2x−4y−15=0 Napisz równanie stycznej do tego okręgu przechodzącej przez punkt B(3,4)

Michał : (x²+2x+1)−1+(y²−4y+4)−4−15=0 (x+2)²+(y−2)²=20 S(−2,2) r=2√5 l:y=ax+b ⇒ 2=−2a+b kolejne równanie układasz tak że odległość srodka od prostej l ma równać się promieniowi okręgu ... powinno wyjsc

Efka: a S to nie jest (−1,2) ? dziękuję, już przeliczam

Michał : tak... masz racje (−1,2)

Mickej : ja preferuje to (x₁ + 2)(x + 2) + (y₁ − 2)(y − 2) = 20 x₁=3 y₁=4 (x+2)²+(y−2)²=20 taki układ równań

Mickej : no to u mnie też jest błąd bo nie sprawdzałem zaufałem naszemu Michałkowi ale to wystarczy zamienić

Michał : widzisz... ja też potrafię irytować

Mickej : no fakt przynajmniej w takich zadaniach byś nie robił błedów

Michał : dobrze ze jesteś czujny misiu kolorowy bo gdyby nie Ty to ciężko by było

Mickej : czemu misiu? romans sie tu kroi

Efka: to jak wtedy wyglada, bez bledu, drugi uklad rownan? bo w tym pierwszym sie nie lapię...

Michał : y=−a+b

Mickej : patrz rozpisujemy sobie równanie okręgu w taki sposób (x−x₁)(x+1)+(y−y₁)(y−2)=20 gdzie x₁ i y₁ to punkty które należą do prostej a drugie równanie to równanie okręgu które znasz

Efka: ok, dzieki pogubilam sie, ale juz ok

Bogdan: x² + y² + 2x − 4y − 15 = 0, B = (3, 4) Środek okręgu S = (−1, 2), x_o = −1, y_o = 2 Długość promienia okręgu R = √1 + 4 + 15 = √20 Równanie okręgu w postaci kanonicznej (x + 1)² + (y − 2)² = 20 Sprawdzamy, czy punkt B należy do okręgu: 9 + 16 + 6 − 16 − 15 = 0. Tak, punkt B należy do okręgu. Mamy napisać równanie stycznej do okręgu zawierającej punkt B. Przypominam wzór stycznej okręgu przechodzącej przez punkt B(x_B, y_B) leżący na okręgu: (x_B − x_o)(x − x_o) + (y_B − y_o)(y − y_o) = R² (3 + 1)(x + 1) + (4 − 2)(y − 2) = 20 4x + 4 + 2y − 4 − 20 = 0 4x + 2y − 20 = 0 /:2 => 2x + y − 10 = 0 postać ogólna stycznej y = −2x + 10 postać kierunkowa stycznej