Znajdź równania wspólnych stycznych do okręgów
Trix: Napisz równania wspólnych stycznych do okręgów:
x2+y2=1 oraz (x−4)2+y2=1
Mam problem z znalezieniem jakiegokolwiek równania stycznych do okręgu, to jest zadanie
przykładowe.
Co zrobiłem z tym zadaniem?
Na początek wyliczyłem S1 oraz S2, S1=(0,0) S2=(0,4) oraz R1, R2 i okazało się, że
R1=R2, więc z tego wynika, że okręgi mają 3 wspólne styczne, co dalej?
26 kwi 23:35
123: Ale styczne do 2 równocześnie, czy styczne do każdego z osobna?
26 kwi 23:41
MQ:
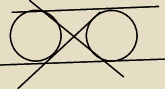
Nie trzy, tylko cztery:
26 kwi 23:41
123: A wspólnych, czyli od obu równocześnie

Źle przeczytałem

26 kwi 23:42
Trix:
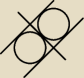
3 styczne do dwóch okręgów jednocześnie
26 kwi 23:44
MQ: Okręgi nie są styczne i leżą na zewnątrz siebie, więc będą 4 styczne.
BTW S1 dobrze, ale S2 źle: powinno być (4,0)
26 kwi 23:46
Trix: UP: A tak, źle przepisałem.
26 kwi 23:48
Mila: zrób rysunek
S2=(4,0)
y=1
y=−1 to dwie styczne
styczne y=ax+b przechodzą przez punkt (2,0) Znajdz punkty styczności:
to będą punkty przecięcia okręgu: (x−2)2+y2=1 z jednym i drugim okręgiem.
26 kwi 23:52
MQ:
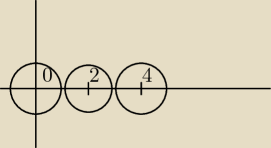
(x−2)
2+y
2=1 nie przecina tych okręgów − jest do nich zewnętrznie styczny:024
26 kwi 23:58
MQ: To 024 na końcu tekstu, to jakieś duchy z rysunku.
27 kwi 00:01
Eta:
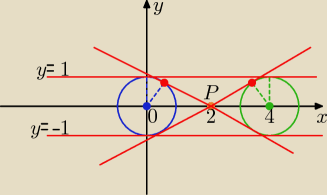
Dwie styczne: y=1 , y= −1
trzecia i czwarta styczna ma równanie
y=ax+b i zawiera P(2,0) ⇒ 0=2a+b ⇒b= −2a
y= ax−2a w postaci ogólnej ax−y−2a=0
Odległość d środka S(0,0) od stycznej jest d=r=1
dokończ wyznacz "a" i następnie "b"
i podaj równania tych stycznych
Powodzenia w rachunkach

27 kwi 00:03
Mila: MQ, trachnęłam się w promieniu, to metoda geometryczna.
27 kwi 00:12
Mila: Jak nie doliczysz się metodą Ety, to napiszę moją. Nie chcę Ci już mącić w głowie.
27 kwi 00:15
Trix: Metoda Ety jest w porządku, wszystko rozumiem, teraz to troszkę rozwinę o obliczenia i spróbuje
kolejne zadania

Dzięki za pomoc.
27 kwi 00:18
Mila: Moja metoda też dobra, ale ostatni okrąg źle.
Oblicz do konca.Masz odpowiedzi?
27 kwi 00:20
Eta:


27 kwi 00:21
Trix: Odpowiedzi nie mam ale przez przypadek znalazłem 2 kolejne metody rozwiązania tego zadania

Wyniki są identyczne.
27 kwi 00:39
Eta:
Bo muszą być

27 kwi 00:42
Mila: Metoda geometryczna:
1) środek odcinka PO (wg oznaczeń z rysunku ETY)
2)w tym przypadku S=(1,0), równanie okręgu (x−1)2+y2=1
3)układ:
(x−1)2+y2=1
x2+y2=1 otrzymujesz punkty styczności...
27 kwi 14:43
 Nie trzy, tylko cztery:
Nie trzy, tylko cztery:
 Źle przeczytałem
Źle przeczytałem 
 3 styczne do dwóch okręgów jednocześnie
3 styczne do dwóch okręgów jednocześnie
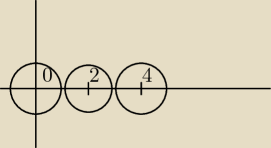 (x−2)2+y2=1 nie przecina tych okręgów − jest do nich zewnętrznie styczny:024
(x−2)2+y2=1 nie przecina tych okręgów − jest do nich zewnętrznie styczny:024
 Dwie styczne: y=1 , y= −1
trzecia i czwarta styczna ma równanie
y=ax+b i zawiera P(2,0) ⇒ 0=2a+b ⇒b= −2a
y= ax−2a w postaci ogólnej ax−y−2a=0
Odległość d środka S(0,0) od stycznej jest d=r=1
Dwie styczne: y=1 , y= −1
trzecia i czwarta styczna ma równanie
y=ax+b i zawiera P(2,0) ⇒ 0=2a+b ⇒b= −2a
y= ax−2a w postaci ogólnej ax−y−2a=0
Odległość d środka S(0,0) od stycznej jest d=r=1

 Dzięki za pomoc.
Dzięki za pomoc.


 Wyniki są identyczne.
Wyniki są identyczne.
