pole olga121: Rozważmy Pięciokąty o obwodzie 2 zbudowane z prostokąta i trójkąta prostokątnego równoramiennego. Jakie największe pole moze mieć taki pięciokąt?

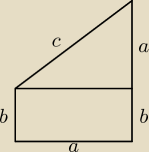
Basia: c = a√2 2a+2b+a√2 = 2 a(2+√2) + 2b = 2

	2−a(2+√2)
b =
	2

	a2		2−a(2 +√2)		a2
P = a*b +		= a*		+		=
	2		2		2

1
	*[ 2a − (2+√2)a2 + a2 ] =
2

1
	*[ a2(−2−√2+1) + 2a ] =
2

−1−√2
	a2 + a
2

ta funkcja osiąga maksimum dla

	−1		1
a = p =		=
	−1−√2		1+√2

pole już sobie sama policz; poza tym rozważ analogicznie inną możliwość (rysunek w następnym wpisie)

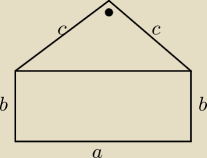
Basia: 2c² = a²

	a
c =
	√2

	2a
a + 2b +		= 2
	√2

a + 2b + a√2 = 2

Skipper:

	1		2√2−1
Chyba Pmax=		=
	1+2√2		7

Basia: nie liczyłam, bo już mi się nie chciało; w końcu to już tylko rachunki