Krawędź podstawy ostrosłupa prawidłowego sześciokątnego ma długośc a oraz kąt mi aqlec: Krawędź podstawy ostrosłupa prawidłowego sześciokątnego ma długośc a oraz kąt miedzy krawędzią boczną a płaszczyzną podstawy wynosi 30. Oblicz pole powierzchni tego ostrosłupa. Wynik wychodzi mi nieprawidłowy. Prosiłabym po obliczenia

aqlec:

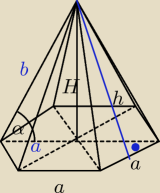
Beti: dane: a, α=30^o

	a2√3		3√3a2
Pp = 6*		=
	4		2

	a
cos α =
	b

√3		a
	=
2		b

	2a		2a√3
b =		=
	√3		3

	1
b2 = (		a)2 + h2
	2

4a2		a2
	=		+ h2
3		4

	16a2		3a2
h2 =		−
	12		12

	13a2
h2 =
	12

	a√13		a√13		a√39
h =		=		=
	√12		2√3		6

	1		1		a√39		a2√39
Pb = 6*		ah = 6*		a*		=
	2		2		6		2

	3√3a2		a2√39		a2(3√3+√39)
Pc = Pp + Pb =		+		=
	2		2		2

aqlec: Dziękuję za pomoc

hahnne: A ja mam pytanko. Wiem, że wyszło dobrze i ładnie to wszystko rozpisane, ale powiedzcie mi tylko proszę, dlaczego moje rozumowanie jest błędne. Otóż mając podane to 30 stopni założyłam sobie (zgodnie z zasadą trójkąta 30,60,90), że krawędź boczna będzie równa 2a, a wysokość a√3...

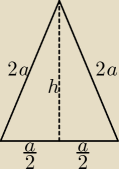
Bogdan: Zawsze zdumiewa mnie obfitość zapisów w rozwiązaniu prostych zadań. Masz hahnne rację. Krawędź boczna ma długość 2a. Wysokość ściany bocznej

	1
h = √4a2 − a2/4 =		a√15
	2

	1		1		1
Pole powierzchni całkowitej P = 6*		a2√3 + 6*		a*		a√15 = ...
	4		2		2

i tyle

Bogdan:

hahnne: No właśnie sobie tak napisałam, jak zaproponowałeś Bogdan to Pc, ale dochodzę do:

	3a2√3		3a2√15
Pc =		+		i mam problem, bo to nie pokrywa się z odpowiedzią :<
	2		2

Bogdan: a widzisz w swoim rozwiązaniu błąd?

hahnne: Kurde. Nie widzę.