Równania i nierówności trygonometryczne Grzegorz: |cosx|= ^√3₂

Grzegorz: Prosze tylko o podanie wyników, nie o rysowanie

nikon: x=π/3+kπ lub x=2/3π+kπ

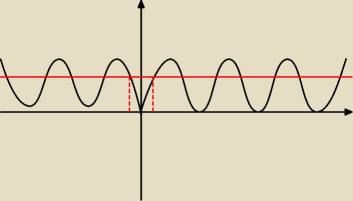
us: nieco krzywy ten cosinus ale to cosinus cosx ≥ 0 cosx<0 cosx = ^√3₂ cosx = − ^√3₂ x= ^π₃ + kπ x= − ^π₃ + kπ gdzie k∊C

nikon: narysowałeś sinusa

Grzegorz: ok a jeszcze mam pytanie o wyniki, jeśli x∊(π;2π) ?

nikon: 4/3π oraz 5/3π

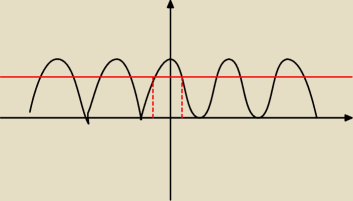
us: racja. mój błąd. dzięki. skupiłem się na trafieniu w kratki...kijowo się rysuje wynik dobry...rysunek poprawnie już :

nikon: mój wynik też dobry jest

Grzegorz: A mógłby ktoś mi wytłumaczyć jak obliczyć wynik jeśli x∊(π;2π) ? Bo mi wychodzą zupełnie inne wyniki

us: @nikon oczywiście Twój też dobry @Grzegorz : po obliczeniu pkt przecięcia (u mnie x= ^π₃ + kπ oraz − ^π₃ + kπ) dobierasz tak stałą K aby wynik zawierał się w żądanym przedziale, czyli wstawiasz k=0, k=1, k=2...k=n dopóty wynik x=.... nie zmieści się w x∊(π;2π). Odpowiedź wyżej podał nikon.

Basia:

	√3		√3
cosx =		lub cosx = −
	2		2

(1) x = ^π₃+2kπ lub x = −^π₃+2kπ lub (2) x = ^2π₃+2kπ lub x=−^2π₃+2kπ podstaw k=1 dostaniesz rozwiązania z przedziału (π;2π) (z 1.2 i 2.2)

Grzegorz: A dlaczego, żeby x∊(π;2π) muszę podstawić k=1 ?

Grzegorz: Od czego to k jest zależne ? jeśli miałbym np przedział x∊(^π₂;π) to ile by to k wynosiło ?

Basia: za k możesz podstawiać dowolne liczby całkowite zasadniczo zaczynasz od 0 i wybierasz co pasuje potem k =1 i k =−1 itd. kończysz jak widzisz, że już "wyskoczyłeś" poza przedział, o który chodzi tutaj: x = ^π₃+2kπ k = 0 ⇒ x=^π₃ za mało czyli idziemy tylko w górę k = 1 ⇒ x=^π₃+2π za dużo czyli koniec x = −^π₃+2kπ k = 0 ⇒ x=−^π₃ za mało czyli idziemy tylko w górę k=1 ⇒ x = −^π₃+2π = ^5π₃ pasuje k=2 ⇒ x= −^π₃+4π = ^11π₃ za dużo czyli koniec i tak dalej