. janko: Dla jakich wartości parametru p wielomian W(x)=5!x⁵+4!px⁴+3!px³ ma co najmniej dwa różne pierwiastki?

Basia: W(x)= x³(5!x² + 4!px + 3!p) jeden pierwiastek x=0 ma musi mieć co najmniej jeszcze jeden czyli Δ = (4!p)² − 4*5!*3!p = p(24²p − 4*120*6) = p(4²*6²p − 4*6*120) = 24p(24p − 120) ≥0 ⇔ p∊(−∞,0>∪<120;+∞)

janko: odpowiedź z ksiazki to p∊(−∞,0>u<5,∞)

Eta: 120x⁵+24px⁴+6px³=0 6x³(20x²+4px+p)=0 Δ= 16p²−80p Δ≥0 ⇒ p²−5p≥0 ⇒ p€ .......... dokończ

janko: p(p−5)≥0 p≥0 p≥5 co nam daje przedział p€ <5,∞) a to ze nalezy od (−∞,0)?

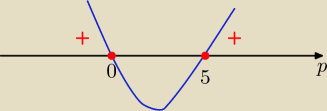
Eta: p(p−5)≥0 x€ (−∞,0> U <5,∞)

ZKS: Jeszcze trzeba chyba 0 wyrzucić ze zbioru rozwiązań.