Arkusz rozszerzony - matematyka rumpek: Arkusz z matematyki rozszerzony zapraszam do "pomordowania" się Zadanie 1 (5pkt) Uzasadnij, że jeżeli trzy liczby naturalne a,b,c tworzą tzw. trójkę pitagorejską (to znaczy: zachodzi równość a² + b² = c²), to co najmniej jedna z nich jest podzielna przez 3. Zadanie 2 (3pkt)

	1
Uzasadnij, że jeżeli x > 0, to x +		≥ 2.
	x

Zadanie 3 (4pkt) Dla jakich wartości parametru m suma kwadratów pierwiastków równania x² − (m − 5)x + 2(3 − m) = 0 jest najmniejsza? Zadanie 4 (5pkt) Wykaż, że funkcja f(x) = log(x + √1 + x²) jest nieparzysta, to znaczy: dla każdego argumentu x należącego do dziedziny funkcji zachodzi równość: f(−x) = −f(x). Zadanie 5 (6pkt)

	3
Rozwiąż równanie: 4tg2x −		* 41/2cos2x = −2, w przedziale x∊<0, 2π>.
	2

Zadanie 6 (4pkt) Trzy liczby dodatnie są kolejnymi wyrazami ciągu geometrycznego. Jeżeli ostatnią zmniejszymy o dwa, to otrzymamy trzy kolejne wyrazy ciągu arytmetycznego. Jeżeli pierwszą liczbę z

	2
otrzymanej trójki powiększymy o		, to znów uzyskamy trzy kolejne wyrazy ciągu
	3

geometrycznego. Wyznacza początkową trójkę liczb. Zadanie 7 (4pkt) W trójkącie ABC, dane są boki: |AC| = 7 i |BC| = 8 oraz miara kąta |∡C| = 120^o. Znajdź długość dwusiecznej kąta C. Zadanie 8 (3pkt) Dany jest okrąg x² + y² = 16 i prosta x − y − 4 = 0. Wyznacz równani okręgu symetrycznego do danego, względem prostej. Zadanie 9 (4pkt) W graniastosłupie prawidłowym trójkątnym pole powierzchni bocznej równe jest sumie pól obu podstaw. Oblicz tangens kąta nachylenia przekątnej ściany bocznej do podstaw graniastosłupa. Zadanie 10 (5pkt) Na odcinku AB o długości 10 obrano punkt M. Odcinek AM stał się bokiem kwadratu, zaś odcinek MB − bokiem trójkąta równobocznego. W jakiej odległości od punktu A należy obrać punkt M, aby suma pól tych figur była najmniejsza? Zadanie 11 (4pkt) Cztery osoby starają się o tę samą posadę. Trzy osoby z zarządu firmy wybierają pracownika w ten sposób, że każda z nich typuje jednego z kandydatów. Kandydat otrzymuje posadę tylko wtedy, jeśli jest wytypowany przez co najmniej dwie osoby z zarządu. Oblicz prawdopodobieństwo, że firma przyjmie pracownika. Zadnie 12 (3pkt) Dana jest funkcja f(x) = x + |x|. a) wyznacz dziedzinę funkcji f b) wyznacz zbiór wartości tej funkcji

Alkain: zad.2

	1
x+		−2≥0 |*x
	x

x²+1−2x≥0 (x−1)²≥0 Koniec

Basiek: Rumpek, witaj, cóż za piękny dzionek. Zrobię w nocy, dzięki Ci wielkie − skąd wytrzasnąłeś?

rumpek: Alkain dałbym 2/3 pkt

Alkain: zad.12 Dziedzina x∊R zbiór wartości Y∊<0,∞)

rumpek: Cześć Basiek, w nowym numerze "Cogito" jest

Alkain: Czemu tylko 2/3 ?;<

rumpek: A gdzie komentarz ? Na maturze za komentarz [uzasadnienie] masz 1pkt

Alkain: Wiem, wiem Ale jakoś mi się nie chciało go pisać to przecież oczywiste, że kwadrat dowolnej liczby jest większy bądź równy zeru

Basiek: Świetnie, miałabym 3pkt A to już 6%... Czas się zbierać do szkoły Do potem, jak mniemam.

rumpek: Jak dla mnie to w tym arkuszu: Zadanie 2, 9, 12 − zbyt proste na rozszerzenie. Natomiast Zadanie 8 jest za zbyt małą ilość punktów. Zadania 5 − nie będzie na maturze bo wyrzucili równania wykładnicze z programu.

lila93: uu no to trzeba rozwiązać

Alkain: Równanie wykładnicze wyrzucili ? Fajnie się dowiedzieć tak kilka dni przed maturką . Z drugiej strony patrząc to poziom matematyki w szkołach coraz niższy...

lila93: @Alkain możesz nam dać szanse ,byśmy sami najpierw rozwiązali

Alkain: Jasne Dlatego więcej już nie pisze...

rumpek: Rozwiązanie z logarytmami przekombinowali − powiem tylko tyle

lila93: wyrzucili? szkodaaa

lila93: o fuuuj. prawdopodobieństwo...no to już wiem,które zad opuścić

rumpek: Czemu, bardzo proste zadanie, tylko treść jest pogmatwana − nic poza tym

lila93: dla mnie nie proste:( akurat wtedy ,gdy omawialiśmy byłam chora,sama trochę ogarnęłam,ale na rozszerz.to zawsze omijam

Alkain: rumpek masz rację zacząłem robić to z tym logarytmem to powiem że ciekawie...

rumpek: Jakie ciekawie 1 linijka i zadanie zrobione, im zajęło 3

lila93: zad 1 to chyba aksjomat jest

Alkain: Ja się w jednej nie zmieściłem :<. Jeszcze muszę ogarnąć 1 zadanie bo nie mam pomysłu jak to udowodnić. Reszta nie specjalnie wymagająca

lila93: nie umiem 4 zad i 1

rumpek: No dobra

Alkain: Rozpisać 4 ?

lila93: tak

rumpek: Zadanie 4 Z: D = R L = f(−x) = log(−x + √x² + 1) = log(√x² + 1 − x)

	1
P = −f(x) = log(x + √x2 + 1)−1 = log(		) = log(√x2 + 1 − x) = L
	√x2 + 1 + x

c.n.u.

Alkain: zad.4 Wykaż, że funkcja f(x) = log(x + √1 + x2) jest nieparzysta, to znaczy: dla każdego argumentu x należącego do dziedziny funkcji zachodzi równość: f(−x) = −f(x). Dziedzina: x+ √1 + x2>0 x∊R f(−x)=−f(x) log(−x+ √1 + x2)=−log(x+ √1 + x2) log(−x+ √1 + x2)log(x+ √1 + x2)⁻¹ −x+√1 + x2=(x+√1 + x2)⁻¹

	1
−x+√1 + x2=		|*(x+√1 + x2)
	x+ √1 + x2

(√1 + x2)²−x²=1 1+x²−x²=1 1=1

rumpek: Przekombinowane

Alkain: Ale się zgadza

rumpek: Tylko ciekawe czy twoje rozwiązanie zaakceptowałoby CKE Bo rok temu jak ktoś [zadanie z prawdopodobieństwem] doszedł do formy P(AuB) ≤ 1, która jest prawdziwa, dostawał 0 pkt, za udowodnienie. Bo wyszedł od tego co miał udowdonić

lila93: log(1−√x² + 1 − x) ← nie wiem co sie stało z tą 1

rumpek: Z jaką jedynką? i który sposób

lila93: @Alkain twoje rozumiem

lila93: @rumpek z tą w logarytmie log(1−√x² + 1 − x)

rumpek:

	1		√x2 + 1 − x
log (		) = log(		= ...
	√x2 + 1 + x		√x2 + 1 * √x2 + 1 − x * x

Po prostu usuwasz niewymierność

rumpek: W moim nie ma żadnego: log(1 − √x² + 1 − x) dlatego się dziwie Co ty szukasz

lila93: ze wzoru.bo można to zapisać też jako różnicę przecież,ale wtedy do niczego nie dojdziemy ..raczej

lila93: dobrze...a zrobił ktoś 1 zad..?

DSGN.: rumpek tu jest arkusik dla Cb https://matematykaszkolna.pl/forum/143137.html

Alkain: Ja na 1 nie mam pomysłu

lila93: wybiera sie ktoś może na budownictwo do Gliwic..?...

rumpek: W Gliwicach mam kuzynkę

rumpek: Zad 1 − dużo do pisania Ale standardowo: 3k + 1, 3k + 2 potem do kwadratu itp.

lila93: 143406

Alkain: Moja koleżanka z klasy do Gliwic chce, ale na architekturę

lila93: ja chodziłam na rysunek przez caluutki roczek by także iść na architekturę ,ale stwierdziłam że wolę jednak coś porządniejszego

lila93: pomoże mi ktoś w tym zadaniu co jest zaznaczone na niebiesko?

rumpek: Napisał ci kolega co masz zrobić w Twoim temacie, Ten temat dotyczy matury, więc jakbyś mogła nie śmiecić

lila93: @rumpek moj kotek siedzi obok mnie i mowi że jesteś niemiły:( a kolega mi bardzo pomógł ,dlatego piszę tutaj:(

rumpek: Zmień kotka

rumpek: Jak dla Ciebie, prośba o niezaśmiecanie tematu jest obraźliwe, to niestety nie ja mam problem.

123: Zad. 3 A) a > 0 m ∊ R B) Δ ≥ 0 [−(m−5)]²−4*1*2*(3−m) ≥ 0 m²−10m+25−24+8m ≥ 0 m²−2m+1 ≥ 0 (m−1)² ≥ 0 m ∊ R C) x₁² + x₂² (x₁ + x₂)²−2x₁x₂

	−b		c
(		)2−2
	a		a

	m−5		2(3−m)
(		)2−2
	1		1

(m−5)²−4(3−m) m²−10m+25−12+4m m²−6m+13 ponieważ a > 0:

	−b
mmin =
	2a

	6
mmin =
	2

m_min = 3 Odp. Dla parametru m = 3 suma kwadratów pierwiastków równania x2 − (m − 5)x + 2(3 − m) = 0 jest najmniejsza.

bitu: zad 8.pomoże ktoś−wskazówki?

kylo1303: rumepk ja nie wiem skad ty to wynajdujesz :0 I ze potem ci sie chce to przepisac/przekopiowac tutaj. Nie bede czytal co pisaliscie bo tez dzisiaj siade i zrobie (nastepna matura do kolekcji). I tak btw to co ty jeszcze zdajesz na maturze? Informatyke? Oczywiscie pomijajac obowiazkowe.

janko: o tak to powinno wygladać oczywiscie ten rysunek nie ma nic wspolnego z danymi z tego zadania ale powinien dac Ci poglada na sprawe czerwona kropka 90^o

janko: jakie macie wyniki do zadania 6?

bitu: @janko,to do mnie?

bitu: mniej więcej,oczywiście promienie te same.

AC: Początkowa trójka: 2; 4; 8

rafi: trzecie równanie do szóstego to (5/3b)² = a(c−2) czy coś źle kombinuje?

rafi: aa okej już wiem, nie b o 2/3 tylko a

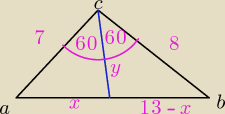
123: Zad. 7 Najpierw z tw. cosinusów obliczyłem najdłuższy bok: |AB|² = 7²+8²−2*7*8*cos120^o

	1
|AB|2 = 49+64−112*(−		)
	2

|AB|² = 49+64+56 |AB|² = 169 |AB| = 13 Potem z układu równań:

⎧	x2 = 72+y2−2*7*y*cos60o
⎩	(13−x)2 = h2 + 82 −2*h*8*cos60o

wychodzi, mniej więcej: 225y²−1680y+3136=0 Δ = 2822400−2822400 = 0

	1680		56
y0 =		=
	450		15

	56
y0 =		≈ 3,73 − tyle wynosi dwusieczna kąta
	15

123: Zamiast "h" powinno być "y". Nie wiem dlaczego wpisałem "h"...

rafi: w 8 wydaje mi się, że trzeba obliczyć prostą prostopadłą do podanej, następnie znaleźć punkt przecięcia tych dwóch prostych i to będzie (2,−2) i następnie za pomocą wektora obliczyć drugi środek, promień będzie ten sam lub drugi sposób zrobić że środek okręgu pierwszego z drugim tworzy odcinek z drugim środkiem o początku w pkt (0,0) i środku (2,−2), podłożyć pod wzór i mamy

123: Co do zad 8 to trzeba zrobić tak (chyba): 1. wyznaczamy równanie prostej prostopadłej do x−y−4=0 i przechodzącej przez punkt s₁ − środek danego okręgu 2. współrzędne środka równania drugiego symetrycznego okręgu będą spełniały równanie prostej prostopadłej 3. odległość środka okręgu danego w zadaniu od prostej x−y−4=0 równa się jak odległość współrzędnych środka równania drugiego symetrycznego okręgu do tej same jprostej 4. promień taki sam

rafi: drugi sposób zrobić że środek okręgu pierwszego tworzy odcinek z drugim środkiem*

123: Zad. 8 S₁(0, 0) x − y − 4 = 0 ⇒ y = x − 4 r = 4 Robimy tak jak mówiłem: A) y = −x + b 0 = 0+b b = 0 y = −x − prosta prostopadła B) S₂(x, −2)

|0*1−1*0−4|		|x*1−1*(−x)−4|
	=
√12+(−1)2		√12+(−1)2

|0−0−4|		|x+x+4|
	=
√1+1		√1+1

|−4|		|2x+4|
	=		/ *√2
√2		√2

|−4| = |2x+4| 4 = |2x+4| 2x+4 = 4 v 2x+4 = −4 2x = 0 v 2x = −8 x = 0 v x = −4 wychodzi 0 bo okrąg podany w zadaniu drugi okrąg to: x = −4 y = −(−4) = 4 o₂: (x+4)² + (x−4)² = 16

123: Zamiast S₂(x, −2) miało być: S₂(x, −x)

123: To z prawdopodobieństwem ciekawe: Zad. 11 |Ω| = (C¹₄)³ = 4³ = 64 − każdy z szefów może dokonać 1 z 4 możliwych kandydatów, a ponieważ jest 3 dyrektorów to do 3 potęgi A − zdarzenie polegające na dostaniu pracy przez kandydata Komu by się chciało to liczyć. Postąpmy prościej. Jakie jest prawdopodobieństwo, że kandydat nie zostanie wybrany To proste: A' − zdarzenie polegające na tym, że nie zostanie wybrany żaden kandydat

	4*3*2
|A'| = C34*3! =		*3*2 = 24 − C34, ponieważ jest 4 kandydatów a wyboru dokonuje
	3*2

tylko 3 prezesów, dlatego jeden zawsze zostanie pominięty, jeśli ma nie dojść do wybrania pracownika a 3!, ponieważ są 3 po kolei wybory i mogą być 3 możliwości (inczej 3 ustawienia)

	24
P(A') =		− prawdopodobieństwo, że nie zostanie wybrany żaden pracownik
	64

	24		40
P(A) = 1 −		=		− prawdopodobieństwo, że zostanie wybrany pracownik
	64		64

123: Zad. 12 Dla x ≥ 0 f(x) = x+x = 2x Dla x < 0 f(x) = x−x = 0 Po prowizorycznym narysowaniu dla wyznaczonych przedziałów wynika, że: Df = R ZW = <0, +∞)

mer45: Pomoże ktoś https://matematykaszkolna.pl/forum/143450.html

Godzio: Mam nadzieję, że nikt się nie przyczepi że porobię sobie parę zadań

Basiek: Godzio, Ci dzisiejsi maturzyści, to coraz starsi

Godzio: Dużo mi nie zostało, 5 najpierw, a później zobaczymy, przydałoby się nad pierwszym pomyśleć

Godzio:

	π
D = {x : x ∊ R − {		+ kπ}, k ∊ C }
	2

	3
4tg2x −		* 41/(2cos2x) = −2 Niedokładny zapis
	2

	1		3
41/cos2x *		−		* 41/(2cos2x) = − 2 /* 4
	4		2

4^1/cos2x = t > 0 t² − 6t + 8 = 0 (t − 4)(t − 2) = 0 4^1/cos2x = 4 lub 4^1/cos2x = 2

1		1		1
	= 1 lub		=
cos2x		cos2x		2

cos²x = 1 lub cos²x = 2 −− sprzeczność cosx = 1 lub cosx = −1 x = 2kπ lub x = π + 2kπ Łącząc otrzymujemy: x = π + kπ gdzie k ∊ C Znajdujemy rozwiązania w przedziale: x ∊ {0, π,2π}

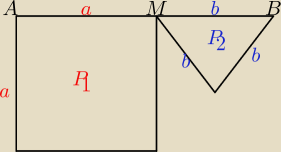
Święty: a,b>0 a+b=10 a=10−b a>0 ⇒ b<10 Pc=P₁+P₂ P₁=a²

	b2√3
P2=
	4

	b2√3
Pc=a2+
	4

	b2√3
Pc=100−20b+b2+
	4

	4+√3
Pc=(		)b2−20b+100
	4

	20
bw=
	4+√3   2*   4

	40(4−√3)
bw=
	13

	10(4√3−3)
a=
	13

	10(4√3−3)
Odp. a=
	13

123: Do zadania pierwszego można skorzystać z tego: a = m² − n² b = 2mn c = m² + n² i m > n i m i n są liczbami pierwszymi co by się nie podstawiło zawsze da się podzielić przez 3 tylko jakoś to trzeba wykazać

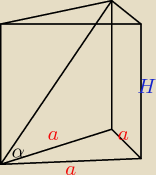
Święty: a,H>0 Pb=2Pp

	a2√3
3aH=2*
	4

6aH=a²√3

	a√3
H=
	6

	H
tgα=
	a

	√3
tgα=
	6

	√3
Odp. tgα=
	6

Vax: 1) Zauważmy, że dla całkowitego a, liczba a² przy dzieleniu przez 3 daje resztę 0 lub 1, jeżeli nie wprost żadna z liczb nie była podzielna przez 3, to lewa strona przy dzieleniu przez 3 dawałaby resztę równą 2, czyli prawa strona nie mogłaby być kwadratem sprzeczność. Warto zauważyć, że analogicznie można pokazać, że któraś z liczb a,b,c dzieli się przez 4, oraz, że pewna z nich dzieli się przez 5

rumpek: No to jedziemy Godzio o dziwo źle Święty źle 123 zadanie 11 źle

rumpek: A nie, jednak 123 prawdopodobieństwo ma dobrze źle spojrzałem

Święty: Wrzuciłbyś prawidłowe wyniki?

Tomek.Noah: Tam u Godzia chyba powinno byc w równaniu zparametryzowanym t²+4t−3=0

Tomek.Noah: Ty wróć źle zapisałem...

Tomek.Noah: t²+8t−6=0

rumpek: Teraz tak patrze to ty Święty też ma dobrze, tylko te wyniki powyciagane i nieskrócone mnie zmyliły Ale Godzio ma niepoprawnie na 100%

Święty: Uff, wstyd byłoby sknocić takie zadanka nie tylko na maturze, ale i tutaj

Tomek.Noah: dobra to licze to zadanie z wykladniczej

matroz: Co do zad 1. jeśli zrobię tak: zakładam że żadna nie jest podzielna przez 3 każda ma postać 2k+1 lub 2k+2 dla k∊N Będzie tu 6 kombinacji porozdzielania 2k+1 i 2k+2 dla a², b², c² rozwiązuję wszystkie kombinacje i wykazuję sprzeczność Z obliczeń wnioskuję że jeśli żadna nie jest podzielna przez 3 to nie jest to trójka pitagorejska dobrze?

Eta: Hehe ........ no i "roztrzaskane" Tak trzymać ......... na maturze

rumpek: 2k + 1, 2k + 2 − ? WTF, chcesz wykwazać podzielność przez dwa? Natomiast warunek 2k + 2 nie ma sensu

matroz: to ma być 3k+1 3k+2 tak?

rumpek: zgadza się

matroz: rumpek to jeśli zrobię tak jak pisałem z tym 3k zamiast 2k to bd ok?

Tomek.Noah:

	3
4tg2x−		*41/2cos2x=−2
	2

	sin2x		1−cos2x		1
tg2x=		=		=		−1
	cos2x		cos2x		cos2x

1		3
	*41/cos2x−		*41/2cos2x=−2
4		2

4^1/cos2x=t, t>0.

1		3
	t−		√t+2
4		2

t−6√t+8=0 √t=u => t=u² u²−6u+8=0 (korzystam z tego c opoliczył Godzio) u=4 v u=2 t=16 v t=4 (pamietam że t bylo >0) zatem: 4^1/cos2x=16 v 4^1/cos2x=4

1		1
	=2 v		=1
cos2x		cos2x

	1
cos2x=		v cos2x=1
	2

	√2		√2
cosx=		v cosx=−		v cosx=1 v cpsx=−1
	2		2

wartości te łatwo policzyć ,

Tomek.Noah:

	π		3		5		7
czyli x∊{0,		,		π,π,		π,		π,2π}
	4		4		4		4

kaś: Zostawcie te zadania tylko pomóżcie tym co naprawdę potrzebują pomocy

123: A co jeśli chodzi o sposób rozwiązania zadania nr 7, 8 i 12 hmm? W ty mroku zdaję maturę także nie jestem nieomylny

Tomek.Noah: w 12 x∊ℛ y≥0

kaś: Jesteście niemożliwi. Ludzie potrzebują pomocy a wy zamiast im pomóc to gadacie o tym, że napiszecie maturę na 90%

Tomek.Noah: poprostu w 12 tak bedzie

	⎧	0 x<0
f(x)=	⎩	2x x≥0

matroz: a ja ponawiam pytanie co do 1. zadania bo umieram z ciekawości

śak: Właśnie po to rozwiązują te zadania i konsultują ich wyniki z innymi aby mieć te 90%... Nie dla każdego szczytem marzeń jest wylewanie cementu na budowie lub kopanie rowów po godzinach...

Tomek.Noah: a co do analitycznej to ja robie tak y=x−4 O₁: x²+y²=16 czyli O(0,0) r=4 "nowy" okrąg będzie mieć promień rowny też 4 dalej znajduje równanie prostej prostopadłej do y=x−4 i przechodzącą przez oba srodki okręgów a zatem y'=−x znajduje ich część wspólną czyli punkt C(2,−2) licze wektor OC=[2,−2] i teraz od pkt C przesuwam go o ten wektor i znajduje wspolrzedne srodka nowego okregu czyli o(4,−4) o: (x−4)²+(y+4)²=16

mer45: Pomożecie https://matematykaszkolna.pl/forum/143450.html

elpe: mozna tez ze pkt C jest środkiem odcinak S₁S₂ gdzie S₁=środek 1 a S₂ srodek 2 S₁=(0,0) S₂=(x,y)

	x+0		y+0
wiec C(2,−2)→		=2 x=4		=−2
	2		2

chyba najprosciej

Tomek.Noah: też mi się tak wydaję

Godzio: No tak, podstawienie było 4^1/(2cos2x) a nie 4^1/cos2x, ale fail wstyd się pokazywać teraz

mer45: pomożecie?

Tomek.Noah: Nie Godziu kazdemu moglo sie zdarzyc nawet Tobie (ale studentowi i nie powiem na jakim kierunku to faktycznie fail xD) zart

mer45: obliczyłem już te boki, ale nie wiem co dalej

Godzio: No, dlatego wracam do topologii Za dużo tych podstaw

zdemotywowany: rumpek, podali odpowiedzi do tych zadań? Mógłbyś je podać?

rafi: 7 wydaje mi się żę dobrze wyliczył 123 bo mam tak samo

rafi: mam pytanie wyliczyłem x wierzchołka w 10 i co dalej z tym zrobić?

Cocacola: 123: B) S2(x, −x) |0*1−1*0−4 |=|x*1−1*(−x)−4| i oczywiście mianownik, ale dlaczego tam jest ta pogrubiona 4 ?

kylo1303: 1. Trudne 2. Łatwe 3. Standardowe 4. Łatwe, trzeba znać podstawowe działania w logarytmach 5. Nadające się na mature (połączenie trygonometrii z f. wykładnicza, sprawiloby to pewnie problemy) 6. Taki o sobie, układ równań 7. *** (patrz niżej) 8. Zadanie łatwe, prosta prostopadła i wektory 9. Łatwe 10. Łatwo wpaść na pomysł, nieprzyjemne liczby 11. Nadające się na mature (podam rozwiazanie inne niz wymienione wyzej, wg. mnie latwiejsze) 12. Proste, ale mozna latwo sie zlapac. *** Z zadaniem 7dmym mialem maly problem. Wyszly mi bowiem 2 wyniki, w ktorym jeden jest prawidlowy, ale drugiego nie moglem odrzucic i nie do konca skad sie wzial. Licze bok AB z tw. cos: AB=13

	x		7
Korzystam z tw. o dwusiecznej:		=		, gdzie x i y to odcinki na ktore dzieli bok AB
	y		8

dwusieczna kata C. Z tego moge wyliczyc x i y:

	91
x=
	15

	104
y=
	15

I teraz zastosowalem tw. cosinusow w jednym z malych trojkatow, i wyszlo mi cos takiego:

	16
z2−8z+16−		=0 , gdzie z to dlugosc dwusiecznej. Z tego mam rozwiazania takie:
	225

	56		64
z1=		i z2=
	15		15

I teraz moje pytanie: skad mi sie wziely dwa wyniki? Pierwszy jest dobry. Ale skoro mam w trojkacie podane 2 boki i kat to nie wiem jak mogl mi trzeci bok wyjsc na dwa sposoby. Moze mi cos umyka, czegos nie widze− w takim razie prosze o sprostowanie. Dodam tylko ze mozna policzyc tw. cos dla drugiego trojkata, i wtedy tez wyjda dwa wyniki:

	49		56
z3=		i z4=		=z1 → z tego wnioskuje poprawnosc rozwiazania (wynik taki sam jak
	15		15

u kogostam wyzej). No i jeszcze obiecane Zadanie 11: |Ω|=4³=64 Rowniez policze A' − zdarzenie ze nie zostanie wybrany, tylko w inny sposob, bardziej przystepny: |A'|=4*3*2=24 Bo pierwsza osoba z zarzadu moze wybrac kazdego z 4 kandydatow, druga juz tylko ktoregos z 3 pozostalych, a ostatni z 2ojki co zostali .

	24		3
P(A')=		=
	64		8

	5
P(A)=
	8

kylo1303: Jakby co to moje pytanie wyżej apropo 2och rozwiazan juz nieaktualne (taka chwilowa tepota mi sie trafila). Takze nei wysilajcie sie z tlumaczeniem.

123: ciekawe, jak każdy rozumuje all inaczej ^^ − grunt, że dobrze

Basiek: Korzystając z okazji, że temat jest dość "maturalny"− gratuluję średniego wykształcenia

rumpek:

kylo1303: Taa... wszyscy mozemy juz kopac doly, stac na kasie, przeprowadzac ludzi przez jezdnie i wiele, wiele innych.

Basiek: kylo, myślę, ze nie z takim wykształceniem.

rumpek: Jeszcze matury brakuje tylko

rumpek: A potem do KFC

rumpek: Albo na zmywak po studiach

Basiek: Myślę, ze z maturą też ciężko będzie Ale wiecie co? Tak strasznie, straaasznie się cieszę, że już koniec. Ogarnianie tego bajzlu strasznie mnie już denerwowało. A teraz... koniec

rumpek: Ja ponad miesiąc temu miałem koniec

Basiek: Ja jeszcze ostatnia prosta wczoraj i dziś. Kupić kwiatki, prezent, iść ze sztandarem, wczoraj jeszcze jakieś ognisko...., wszystko na ostatnią chwilę. Przez te 3 lata stałam się kłębkiem nerwów. To niesamowite, jak ja zasłużyłam na odpoczynek

rumpek: No ja wczoraj nie miałem ogniska do wyjście do pubu . W betonowej dżungli, nie ma gdzie zrobić ogniska

rumpek: Coś czuję, że jutro jakiś arkusz z matmy ułożę

Basiek: Ech... u nas to wygląda tak, że przy szkole jest kilkanaście metrów dalej rzeka. Takie osiedle, rzeka... taka typowa można powiedzieć− żulnia. Tam się chodzi na lektoratach... pić. Na wczorajszym ognisku też nikt nie pomyślał o jedzeniu..., smutna sprawa. A ostrzegali mnie, kiedy szłam na matfiz

rumpek: żulnia żulerstwo

Basiek: Już koniec. Ale mogę powiedzieć, że zostałam dobrze przygotowana do stereotypowego studenckiego życia Już nic mnie nie zdziwi chyba. Przydałoby się dotknąć Aksjomatu chyba, prawda?

rumpek: Nie Czytam streszczenie Wesela, co dokładnie o tej lekturze możesz rzec ?

Basiek: Ooo, moja znienawidzona lektura Można o niej rzec, że... jest dramatem, który jest syntezą wielu sztuk. Ma wiele symboli, które trzeba znać; poza tym... rysy bohaterów utworu są zaczerpnięte z rzeczywistości, więc ich pierwowzory należałoby również poznać

rumpek: Strasznie nudna, nawet streszczenie niezbyt miło się czyta. Zdecydowanie lepsi ludzie bezdomni

Basiek: Judym z Joasią Podborską! Kojarzę gościa. Wiem, że go nie lubię i jest strasznym tchórzem.

rumpek: Udowodnij, że Tomasz Judym jest tchórzem.

Basiek: Poproszę odpowiedni fragment do tematu.

rumpek: Określiłaś go tchórzem bez przywołania fragmentu, także męcz się bez fragmentu

Basiek: Spryciarz. Judym był tchórzem, gdyż całe życie przed czymś uciekał, przed wspomnieniami, przed swoją przeszłością, bał się jej stawić czoło i spojrzeć na nią z perspektywy człowieka dorosłego. Szczególnym tchórzostwem wykazał się (w moim mniemaniu), kiedy zostawił Joannę, gdyż BAŁ SIĘ, że obudzi się w nim "dorobkiewicz", zaryzykował szczęście swoje i (ponoć) ukochanej kobiety tylko i wyłącznie z powodu jakichś wyimaginowanych () lęków. Faceci...

rumpek: 1. Nie każdy facet jest taki sam 2. Zgodzę się z tylko 2,3,4 linijką 3. Nie uciekał przed czymś, tylko chciał zrealizować swoje plany, które były ciulowe.

Basiek: 1) Wcale tak nie twierdziłam, w gruncie rzeczy, to bardziej rozumiem facetów, niż kobiety. 2) Co jest nie tak z resztą? 3) Rumpek− czytałeś książkę? Bo ja tak do połowy doszłam... i naprawdę− gość zwyczajnie ucieka, przy okazji ma te swoje plany..., ale one wszystkie są wynikiem jego przeszłości, dzieciństwa z ciotką. Nie jest to może napisane wprost, ale toż to widać na pierwszy rzut oka.

rumpek: No ja bym nie czytał Akurat Ludzi bezdomni − audiobook

Basiek: To brak mi argumentów. Mam po prostu takie wrażenie. Możesz się nie zgadzać, to jasne. Nie ma klucza= nie ma poprawnej odpowiedzi.

rumpek: Klucz = brak wiedzy; trzeba korzystać z danego intelektu

Basiek: Czasem intelekt w przypadku j. polskiego nie pomaga. Dla mnie śmiesznym jest, że w kluczu czasem wyróżnione są rzeczy, które ja szczerze uważam za ... debilizmy. Inaczej nazwać to ciężko. Z jednej strony "nie przepisuj tekstu" z drugiej− nagle w porównaniu z kluczem, okazuje się, że przydałoby się dosłownie wszystko przepisać.

rumpek: Pierwsze zdanie − trzeba być indywidualistą, dlatego nie lubię polskiego. Bo nie ma dokładnej recepty na zinterpretowanie danego tekstu, każdy ma indywidualne podejście. Człowiek jest istotą rozumną, więc każde zdanie powinno mieć sens. A takie pisanie matury pod klucz jest strasznie chore, nie przynosi nic dobrego. Kiedyś czasy edukacji były bardziej ciekawsze od tych. A odnośnie tych debilizmów to się zgodzę, siedzą jełopy w CKE i tyle. Wszystko zależy od klucza, nastawienia człowieka, dnia w którym piszemy i od Boga [najważniejsze].

Saizou : Witam Kiedyś już śp. Szymborska pisała maturę ze swoich tekstów i..... zdała ją bardzo kiepsko, albo w ogóle nie zdała. Kto jak kto, ale poeta chyba najlepiej wie o czym pisze

rumpek: 66% miała bodajże

Basiek: Saizou− to po prostu inny poziom edukacji. Stąd jej odp. nie zgadzały się z kluczem. To tak jakby w podstawówce napisać działanie : 1+3+4+5=...., a ktoś policzył to za pomocą ciągu arytm., tego też nie byłoby w kluczu

Saizou : ale powinna mieć 100% przecież z własnych tekstów pisała, ale oczywiście szanowne osoby do układania matury nie zwracają uwagi na to. Masz interpretować tak jak oni chcą i tyle

Saizou : http://atrapa.net/legendy/nowa-matura.htm a tutaj artykuł o maturze Szymborskiej

Basiek: Z czego wynika, że wszyscy powtarzają bujdę na kółkach. Co do tekstów w pierwszej części arkusza, wszystko możliwe. Też zazwyczaj nie ogarniam klucza do tego. Mam własną interpretację

Saizou : popieram Ciebie Basiuniu co do własnych interpretacji ja też mam własne i niepowtarzalne. Według mnie matura z polskiego powinna sprawdzać zdolności rozumienia tekstu czytanego, a nie interpretacji, która ci się w życiu nie przyda

Basiek: Błażejku, może i powinna. Nie wiem, ja tu za tydzień to napiszę i będę mieć z głowy. Na zawsze. Już nawet nie rozmyślam nad bezsensem tego. Świadectwo jest, matura też musi być. A potem... się zobaczy.

k: czy w zadaniu 6 odpowiedź to: 2 4 8 ?

Henio: "1/4*4^1/cos2x−3/2*4^1/2cos2x=−2 4^1/cos2x=t, t>0. 1/4t−3/2√t+2=0" Może mi ktoś powiedzieć jak 4^1/2cos2x zamienia się na √t.

Tomek.Noah: masz 4⁽1/cos²x)*1/2=t^1/2=√t

Henio: Dzięki już rozumiem