geometria
heeeeeeelp: w Trójkątach ABC i A1B1C1 poprowadzono dwusieczne CD i C1D1. Uzasadni, że trójkąt
ABC jest przystający do trójkąta A1B1C1, wiedząc, że |CD| = |C1D1|, |DA| = |D1A1|
oraz |kątCDA| = |kąt C1D1A1|
21 kwi 18:46
lisek:
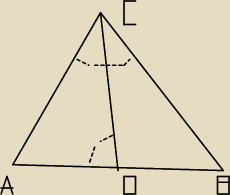
Skoro |CD|=|C
1D
1| i |DA|=|D
1A
1| oraz |kątCDA|=|kątC
1D
1A
1| to |AC|=|A
1C
1| np. z
twierdzenia cosinusów:
|AC|
2=|AD|
2+|CD|
2−2|AD||CD|cos|kątADC|
Również z tw. cosinusów można obliczyć, że |kąt CAB|=|kątC
1A
1B
1|
........................
|kątCDB|=|kątC
1D
1B
1|=180−|kątCDA|
Skoro |CD|=|C
1D
1| jest dwusieczną to |kątACD|=|kątDCB|
Z ΔDBC:
180−180+|kątCDA|−|kątDCB|=|kątABC|=|kątA
1B
1C
1|
W takim razie na podstawie cechy przystawania trójkątów KBK (
czyli |kąt CAB|=|kątC
1A
1B
1| oraz |AC|=|A
1C
1| oraz |kątABC|=|kątA
1B
1C
1|) wynika,
że trójkąty ABC i A
1B
1C
1 są przystające
21 kwi 19:29
Eta:
Mozna prościej, np. tak:
< BAC = <B
1A
1C
1 −− bo są wspólne
<ACD= <A
1C
1D
1 −−− bo z dwusiecznej
więc trzeci kąt w ΔADC i wΔA
1D
1C
1 musi być równy
zatem z cechy II ( b,kb) ΔACD przystakje do ΔA
1C
1D
1
podobnie w trójkątach BCD i B
1C
1D
1
tym razem z cechy III (k,bk)
bo <BDC= <B
1D
1C
1 = 180
o − <ADC
i <BCD =,B
1C
1D
1 −−− z dwusiecznej
i ICDI= IC
1D
1I czyli ΔBCD przystaje do trójkata B
1C
1D
1
czyli ΔABC przystaje do ΔA
1B
1C
1
i nie potrzeba wzoru cosinusów

21 kwi 20:05
heeeeeeelp: dzięki Eta.
21 kwi 21:08
 Skoro |CD|=|C1D1| i |DA|=|D1A1| oraz |kątCDA|=|kątC1D1A1| to |AC|=|A1C1| np. z
twierdzenia cosinusów:
|AC|2=|AD|2+|CD|2−2|AD||CD|cos|kątADC|
Również z tw. cosinusów można obliczyć, że |kąt CAB|=|kątC1A1B1|
........................
|kątCDB|=|kątC1D1B1|=180−|kątCDA|
Skoro |CD|=|C1D1| jest dwusieczną to |kątACD|=|kątDCB|
Z ΔDBC:
180−180+|kątCDA|−|kątDCB|=|kątABC|=|kątA1B1C1|
W takim razie na podstawie cechy przystawania trójkątów KBK (
czyli |kąt CAB|=|kątC1A1B1| oraz |AC|=|A1C1| oraz |kątABC|=|kątA1B1C1|) wynika,
że trójkąty ABC i A1B1C1 są przystające
Skoro |CD|=|C1D1| i |DA|=|D1A1| oraz |kątCDA|=|kątC1D1A1| to |AC|=|A1C1| np. z
twierdzenia cosinusów:
|AC|2=|AD|2+|CD|2−2|AD||CD|cos|kątADC|
Również z tw. cosinusów można obliczyć, że |kąt CAB|=|kątC1A1B1|
........................
|kątCDB|=|kątC1D1B1|=180−|kątCDA|
Skoro |CD|=|C1D1| jest dwusieczną to |kątACD|=|kątDCB|
Z ΔDBC:
180−180+|kątCDA|−|kątDCB|=|kątABC|=|kątA1B1C1|
W takim razie na podstawie cechy przystawania trójkątów KBK (
czyli |kąt CAB|=|kątC1A1B1| oraz |AC|=|A1C1| oraz |kątABC|=|kątA1B1C1|) wynika,
że trójkąty ABC i A1B1C1 są przystające
