Trójkąt, środkowa Tomek: Trójkąt ma boki długości 10, 6, 12. Oblicz długość środkowej opuszczonej na najdłuższy bok.

psik: dobrze by było zrobić rysunek, ale tu strasznie długo się go robi. Środkowa opuszczona na bok o długości 12 dzieli go na pół czyli na 6 i 6 ( bo to w końcu środkowa) . Powstają nam teraz jakby 2 trójkąty mniejsze. Oznacz sobie środkową jako x, masz też bok 6 i w zależności na który trójkąt spojrzysz bok 10 lub bok 6. Najłatwiej jest chyba z dużego trójkąta ( wyjściowego) obliczyć cos α dla kąta między np bokami 12 i 6. Z tw. cosinusów : cos α = ^{122 + 62 − 102} _2*12*6 = ^144+36−100₁₄₄ = ⁸⁰₁₄₄ ( chyba dobrze ale pewien nie jestem; tu od razu liczyłem cos α, ale możesz zacząć od boku naprzeciwko tego kąta) Możesz skrócić cos α do postaci ⁵₉ i w takiej zostaw, bo żadnej ładnej wartości kąta nie znajdziesz. Teraz patrzysz na mniejszy trójkąt o bokach : x,6,6. Między bokami 6 i 6 masz kąt α. Jest on naprzeciwko boku x. Z tw. cosinusów (drugi raz): x² = 6² + 6² − 2*6*6*cos α = 36 + 36 − 72*⁵₉ = 72 − 40 = 32 z tego wychodzi że x = √32 = 4√2 . Jak źle to krzyczeć.

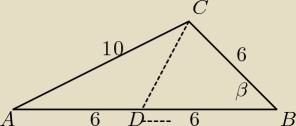Mila: w ΔABC: 10²=12²+6²−2*12*6cosβ

	5
cosβ=
	9

W ΔDBC:

	5
|CD|2= 62+62−2*6*6*
	9

|CD|²=32 |CD|=√32=4√2 Proszę, oto z rysunkiem.