geometria Ssssussssa: Dłuższa przekątna rombu ma długośc d a kat ostry rombu ma miarę 60 stopni. Oblicz stosunek pola kołą wpisanego w ten romb do pola tego rombu. ale takby to d było użyte...

mint: a wiec mysle ze to bedzie tak d− krotsza przekątna D−dluzsza przekątna

	d*D
Pr =		pole rombu
	2

Pk = (¹₄D)²π pola koła wpisanego w romb stosunek

(14D)2π		2
	=		* (14D)2π =
d*D   2		d*D

	2		(18D2π)		(18Dπ)
= 116D2π *		=		=
	d*D		d*D		d

tak mi sie wydaje tylko czy to jest ten stosunek juz?

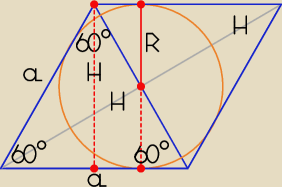
Bogdan: Nie, to nie jest ten stosunek. Może ten rysunek będzie pomocny. d − dłuższa przekątna rombu, d = 2H, e − krótsza przekątna rombu, e = a

	1   d 2		d
a − długość boku rombu,		= sin60o => a =
	a		√3

	1
H − wysokość rombu i wysokość trójkąta równobocznego o boku a, H =		a√3 = 2R
	2

	1
R − długość promienia koła wpisanego w romb, R =		H
	2

dpelczar: Bogdan − mam pytanie − zawsze przekątna rombu dzieli kąt na dwie równe połowy

Bogdan: Przekątne rombu: 1. przecinają się w połowie, 2. przecinają się pod kątem prostym, 3. są dwusiecznymi kątów wewnętrznych rombu.

Ssssussssa: Już czaję, dzięki

Ssssussssa: A można jeszcze poprosić o obliczenie pól i stosunek?

999: rrrrδΔΩ←