trapez Zosia: W trapezie ABCD dlugosc dluzszej podstawy AB=10 oraz dlugosc ramienia AD=6. Dwusieczna kata BAD przecina podstawe DC w punkcie P. oblicz dlugosc krotszej podstawy trapezu, jezeli pole czworokata ABCP jest dwa razy wieksze od pola trojkata ABS, gdzie S jest punktem przeciecia odcinka AP z przekatna DB. Czy mógłby mi ktos pomoc z tym zadaniem? Bardzo proszę

Zosia:

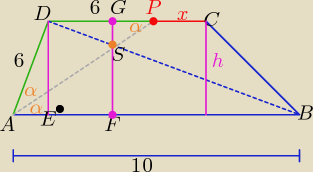
Eta: ΔAPD jest równoramienny to: |DP|=|AD|=6

	10
ΔABS ~ ΔDPS w skali k=
	6

to: |FS|= 10 y i |GS|=6y zatem h=16y , y>0

	10+x		1
Z treści zadania P(trABCP)= 2P(ΔABS) ⇒		*h=2*		*10*|SF|
	2		2

	x+10
		*16y= *10*10y /:y
	2

(x+10)*8=100 x=............. to: |DC|= 6+x=.............

Zosia: skad wiadomo że trojka APD jest rownoramienny skąd ta skala?

Mila: ETA , Pięknie!

Zosia: Też uwazam ze pięknie Dziękuje ale skad wiadomo że trojka APD jest rownoramienny i skąd ta skala?

Eta: Z własności dwusiecznej i z tego,że kąty APD i PAB −−− naprzemianległe ΔABS ~ ΔDPS z cechy (kkk)

	|AB|		10
to: k=		=
	|DP|		6

Eta: Witaj Mila

Zosia: ahaaaaa, dziekuję juz rozumiem

Eta: Na zdrowie

Zosia: jeszcze tylko zapytam co to jest y w obliczeniach?

Zosia: ?

Zosia: ?

Mila: y to jest wspólna miara. GS:FS=6:10 to można zapisać, że : GS=6y, FS=10y

Eta: